
分析 (1)①an+1=|p-an|+2an+p,可得a2=|1-a1|+2a1+1=2-2+1=1,同理可得a3=3,a4=9.
②a2=1,an+1=|1-an|+2an+1,当n≥2时,an≥1,当n≥2时,an+1=-1+an+2an+1=3an,即从第二项起,数列{an}是以1为首项,以3为公比的等比数列,利用等比数列的求和公式即可得出Sn.
(2)an+1-an=|p-an|+an+p≥p-an+an+p=2p>0,可得an+1>an,即{an}单调递增.
(i)当$\frac{{a}_{1}}{p}$≥1时,有a1≥p,于是an≥a1≥p,可得an+1=|p-an|+2an+p=an-p+2an+p=3an,${a}_{n}={3}^{n-1}•{a}_{1}$.利用反证法即可得出不存在.
(ii)当$-1<\frac{{a}_{1}}{p}<1$时,有-p<a1<p.此时a2=|P-a1|+2a1+p=p-a1+2a1+p=a1+2p>p.于是当n≥2时,an≥a2>p.从而an+1=|p-an|+2an+p=an-p+2an+p=3an.an=3n-2a2=3n-2(a1+2p)(n≥2).假设存在2as=ar+at,同(i)可知:r=1.得出矛盾,因此不存在.
(iii)当$\frac{{a}_{1}}{p}$≤-1时,有a1≤-p<p.a1+p≤0.于是a2=|P-a1|+2a1+p=p-a1+2a1+p=a1+2p.a3=a1+4p.即可得出结论.
解答 解:(1)①∵an+1=|p-an|+2an+p,
∴a2=|1-a1|+2a1+1=2-2+1=1,
a3=|1-a2|+2a2+1=0+2+1=3,
a4=|1-a3|+2a3+1=2+6+1=9,
②∵a2=1,an+1=|1-an|+2an+1,
∴当n≥2时,an≥1,
当n≥2时,an+1=-1+an+2an+1=3an,即从第二项起,数列{an}是以1为首项,以3为公比的等比数列,
∴数列{an}的前n项和Sn=a1+a2+a3+a4+…+an=-1+$\frac{1-{3}^{n-1}}{1-3}$=$\frac{1}{2}×{3}^{n-1}$-$\frac{3}{2}$,(n≥2),
显然当n=1时,上式也成立,
∴Sn=$\frac{1}{2}×{3}^{n-1}$-$\frac{3}{2}$;
(2)∵an+1-an=|p-an|+an+p≥p-an+an+p=2p>0,
∴an+1>an,即{an}单调递增.
(i)当$\frac{{a}_{1}}{p}$≥1时,有a1≥p,于是an≥a1≥p,
∴an+1=|p-an|+2an+p=an-p+2an+p=3an,∴${a}_{n}={3}^{n-1}•{a}_{1}$.
若数列{an}中存在三项ar,as,at(r,s,t∈N*,r<s<t)依次成等差数列,则有2as=ar+at,
即2×3s-1=3r-1+3t-1.(*)
∵s≤t-1,∴2×3s-1=$\frac{2}{3}×{3}^{s}$<3t-1<3r-1+3t-1.因此(*)不成立.因此此时数列{an}中不存在三项ar,as,at(r,s,t∈N*,r<s<t)依次成等差数列.
(ii)当$-1<\frac{{a}_{1}}{p}<1$时,有-p<a1<p.此时a2=|P-a1|+2a1+p=p-a1+2a1+p=a1+2p>p.
于是当n≥2时,an≥a2>p.从而an+1=|p-an|+2an+p=an-p+2an+p=3an.∴an=3n-2a2=3n-2(a1+2p)(n≥2).
若数列{an}中存在三项ar,as,at(r,s,t∈N*,r<s<t)依次成等差数列,则有2as=ar+at,
同(i)可知:r=1.于是有2×3s-2(a1+2p)=a1+3t-2(a1+2p),∵2≤S≤t-1,∴$\frac{{a}_{1}}{{a}_{1}+2p}$=2×3s-2-3t-2=$\frac{2}{9}×{3}^{s}$-$\frac{1}{3}×{3}^{t-1}$<0.∵2×3s-2-3t-2是整数,∴$\frac{{a}_{1}}{{a}_{1}+2p}$≤-1.于是a1≤-a1-2p,即a1≤-p.与-p<a1<p矛盾.
故此时数列{an}中不存在三项ar,as,at(r,s,t∈N*,r<s<t)依次成等差数列.
(iii)当$\frac{{a}_{1}}{p}$≤-1时,有a1≤-p<p.a1+p≤0.
于是a2=|P-a1|+2a1+p=p-a1+2a1+p=a1+2p.
a3=|p-a2|+2a2+p=|a1+p|+2a1+5p.=-a1-p+2a1+5p=a1+4p.
此时数列{an}中存在三项a1,a2,a3依次成等差数列.
综上可得:$\frac{{a}_{1}}{p}$≤-1.
点评 本题考查了等差数列与等比数列的通项公式与求和公式、方程的解法、数列递推关系、分类讨论方法、反证法,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:填空题
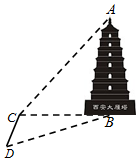 如图,某数学兴趣小组为了测量西安大雁塔高AB,选取与塔底B在同一水平面
如图,某数学兴趣小组为了测量西安大雁塔高AB,选取与塔底B在同一水平面查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 投资股市 | 获利40% | 不赔不赚 | 亏损20% | 购买基金 | 获利20% | 不赔不赚 | 亏损10% |
| 概率P | $\frac{1}{2}$ | $\frac{1}{8}$ | $\frac{3}{8}$ | 概率P | p | $\frac{1}{3}$ | q |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | (-2,3) | C. | (-2,4) | D. | (-2,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | $[\frac{1}{3}$,+∞) | C. | (0,$\frac{1}{3}]$ | D. | (0,$\frac{2}{3}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $2\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
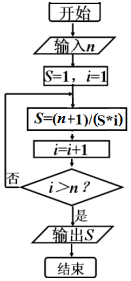
| A. | $\frac{1}{20}$ | B. | $\frac{5}{16}$ | C. | $\frac{16}{5}$ | D. | $\frac{3}{8}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com