
 如图,在四棱锥P-ABCD中,底面ABCD为梯形,CD∥AB,AB=2CD,AC交BD于O,锐角△PAD所在平面⊥底面ABCD,PA⊥BD,点Q在侧棱PC上,且PQ=2QC.
如图,在四棱锥P-ABCD中,底面ABCD为梯形,CD∥AB,AB=2CD,AC交BD于O,锐角△PAD所在平面⊥底面ABCD,PA⊥BD,点Q在侧棱PC上,且PQ=2QC.分析 (1)连接OQ,可得PA∥OQ,即可证得PA∥平面QBD.
(2)在平面PAD内过P作PH⊥AD于H,可得PH⊥平面ABCD,即可得PH⊥BD,可得到以BD⊥平面PAD,即BD⊥AD.
解答 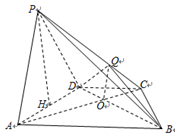 解:(1)如图,连接OQ,因为AB∥CD,AB=2 CD,
解:(1)如图,连接OQ,因为AB∥CD,AB=2 CD,
所以AO=2OC,又PQ=2QC,
所以PA∥OQ,…(3分)
又OQ?平面QBD,PA?平面QBD,
所以PA∥平面QBD.…(6分)
(2)在平面PAD内过P作PH⊥AD于H,因为侧面PAD⊥底面ABCD,平面PAD∩平面ABCD=AD,
PH?平面PAD,所以PH⊥平面ABCD,…(9分)
又BD?平面ABCD,所以PH⊥BD,又PA⊥BD,
且PA和PH是平面PAD内的两条相交直线,所以BD⊥平面PAD,…(12分)
又AD?平面PAD,所以BD⊥AD.…(14分)
点评 本题考查了空间线面平行的判定,线线垂直的判定,考查了转化思想,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
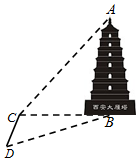 如图,某数学兴趣小组为了测量西安大雁塔高AB,选取与塔底B在同一水平面
如图,某数学兴趣小组为了测量西安大雁塔高AB,选取与塔底B在同一水平面查看答案和解析>>
科目:高中数学 来源: 题型:解答题
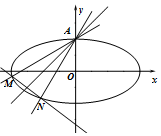 如图,已知直线l:y=kx+1(k>0)关于直线y=x+1对称的直线为l1,直线l,l1与椭圆E:$\frac{x^2}{4}+{y^2}$=1分别交于点A、M和A、N,记直线l1的斜率为k1.
如图,已知直线l:y=kx+1(k>0)关于直线y=x+1对称的直线为l1,直线l,l1与椭圆E:$\frac{x^2}{4}+{y^2}$=1分别交于点A、M和A、N,记直线l1的斜率为k1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 投资股市 | 获利40% | 不赔不赚 | 亏损20% | 购买基金 | 获利20% | 不赔不赚 | 亏损10% |
| 概率P | $\frac{1}{2}$ | $\frac{1}{8}$ | $\frac{3}{8}$ | 概率P | p | $\frac{1}{3}$ | q |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $2\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com