
| m |
| n |
| π |
| 2 |
| m |
| n |
|
| ||
| cosA |
|
| ||
| cosB |
|
| ||
| cosC |
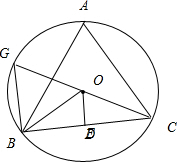
| OD |
| OB |
|
| ||
| cosA |
|
| ||
| cosB |
|
| ||
| cosC |
 解:(Ⅰ)∵
解:(Ⅰ)∵| m |
| n |
| π |
| 2 |
| 1 |
| 2 |
| 1-cos2A |
| ||
| 2 |
| a |
| sinA |
| 2 | ||
|
| ||
| 3 |
| π |
| 3 |
| OD |
| OB |
| OD |
| OB |
|
| ||
| cosA |
|
| ||
| cosB |
|
| ||
| cosC |
|
| ||
| cosA |
|
| ||
| cosB |
|
| ||
| cosC |
| ||
| 3 |
| 3 |


科目:高中数学 来源: 题型:
| ||
| 2 |
| A、(1,4) | ||
| B、(4,+∞) | ||
C、(
| ||
| D、(0,1)∪(1,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 3 |
| π |
| 2 |
| α |
| 2 |
| π |
| 12 |
| 10 |
| 13 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 组号 | 分组 | 频数 | 频率 |
| 第一组 | [230,235) | 8 | 0.16 |
| 第二组 | [235,240) | ① | 0.24 |
| 第三组 | [240,245) | 15 | ② |
| 第四组 | [245,250) | 10 | 0.20 |
| 第五组 | [250,255] | 5 | 0.10 |
| 合 计 | 50 | 1.00 | |
查看答案和解析>>
科目:高中数学 来源: 题型:
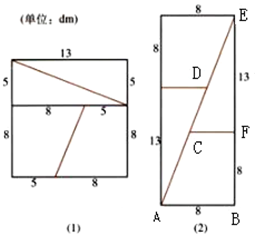 魔术大师把一块长和宽都是13dm的地毯按图(1)裁好,再按图(2)拼成矩形.计算两个图形的面积,分别得到169dm2与168dm2.魔术师得意洋洋的说,他证明了169=168.你能揭穿魔术师的奥秘吗?
魔术大师把一块长和宽都是13dm的地毯按图(1)裁好,再按图(2)拼成矩形.计算两个图形的面积,分别得到169dm2与168dm2.魔术师得意洋洋的说,他证明了169=168.你能揭穿魔术师的奥秘吗?查看答案和解析>>
科目:高中数学 来源: 题型:
 已知椭圆C1:
已知椭圆C1:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com