
分析 (1)令x1=x2,得f(1)=0.
(2)根据单调性的定义证明即可,
(3)先求出f(9)=-2,再根据函数为减函数,即可得到$\left\{\begin{array}{l}{|x|>9}\\{|x|>0}\end{array}\right.$,解得即可.
解答 解:(1)令x1=x2,得f(1)=0.
(2)设任意的x1,x2>0,且x1>x2,则f(x1)-f(x2)=f($\frac{{x}_{1}}{{x}_{2}}$)
又x>1时,f(x)<0,
∴由$\frac{{x}_{1}}{{x}_{2}}$>1,得f($\frac{{x}_{1}}{{x}_{2}}$)=f(x1)-f(x2)<0,即f(x1)<f(x2),
∴函数f(x)在(0,+∞)上是减函数.
(3)由f(3)=-1,f(1)=0,得f($\frac{1}{3}$)=f(1)-f(3)=1,
∴f(9)=f($\frac{3}{\frac{1}{3}}$)=f(3)-f($\frac{1}{3}$)=-2.
∴f(|x|)<-2=f(9)可化为$\left\{\begin{array}{l}{|x|>9}\\{|x|>0}\end{array}\right.$
解得x>9或x<-9.
点评 本题的考点是抽象函数的性质及其应用,根据证明函数单调性的方法,反复给x1和x2值利用给出恒等式,注意条件的利用;求解不等式时利用函数的奇偶性及条件转化为两个函数值的关系,进而由函数的单调性转化为自变量的大小,属于中档题.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:选择题
 如图所示的茎叶图记录了甲、乙两个小组(每小组4人)在期末考试中的数学成绩.乙组记录中有一个数据模糊,无法确认,在图中以α表示.已知甲、乙两个小组的数学成绩的平均分相同,则乙组数学成绩的中位数为( )
如图所示的茎叶图记录了甲、乙两个小组(每小组4人)在期末考试中的数学成绩.乙组记录中有一个数据模糊,无法确认,在图中以α表示.已知甲、乙两个小组的数学成绩的平均分相同,则乙组数学成绩的中位数为( )| A. | 92 | B. | 93 | C. | 93.5 | D. | 94 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
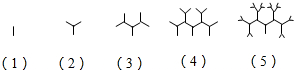 如图所示是按照一定规律画出的一列“树型”图,设第n个图有an个“树枝”,则an+1与an(n≥1)之间的关系是an+1=2an+1(n≥1).
如图所示是按照一定规律画出的一列“树型”图,设第n个图有an个“树枝”,则an+1与an(n≥1)之间的关系是an+1=2an+1(n≥1).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{41}$+1和$\sqrt{41}$-1 | B. | 3和1 | C. | 5$\sqrt{2}$和$\sqrt{34}$ | D. | $\sqrt{39}$和3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f($\frac{5}{2}$)>f(1)>f($\frac{7}{2}$) | B. | f(1)>f($\frac{5}{2}$)>f($\frac{7}{2}$) | C. | f($\frac{7}{2}$)>f($\frac{5}{2}$)>f(1) | D. | f($\frac{7}{2}$)>f(1)>f($\frac{5}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com