
���� �Ԣٿ�������a��b������ƽ��ֱ�ߣ���a��b�������ֱཻ�ߣ�������ƽ���ڵ���Ӱ�������жϣ�
�Ԣڣ���һ��ƽ��ȡ��һ�������壬�������������ཻ��������������ཻ�������жϣ�
�Ԣۣ��ֱ������İ뾶�;��ε����������Բ�İ뾶���ɵ����ĵ�����ľ��룬���������ʽ�����㼴���жϣ�
�Ԣܣ���������ABCD-A1B1C1D1�Ͻ�����ͼ��ʾ�ռ�ֱ������ϵ���������������ⳤΪ1������B1D������B1D����ȡһ��P���������������ⳤΪ1������B1D������B1D����ȡһ��P�����������������ģ���㵽ֱ�ߵľ��룬�����жϣ�
��� �⣺�٣���a��b������ƽ��ֱ�ߣ���a��b��ƽ����ڵ���Ӱ�������������ֱཻ�ߣ�a��b��ƽ����ڵ���Ӱ������ƽ��ֱ�ߣ�����������a��b�������ֱཻ�ߣ���a��b��ƽ����ڵ���Ӱ�����������ֱཻ�ߣ�a��b��ƽ����ڵ���Ӱ������������ƽ��ֱ�ߣ�����������a��b����������ֱ�ߣ��ʢ���ȷ��
�ڣ���һ��ƽ��ȡ��һ�������壬�������������ཻ��������������ཻ������ͼ������������Ρ��ı��Ρ�����Ρ������Σ��ʢ���ȷ��
�ۣ�����ABCD�ĶԽ��߳�Ϊ$\sqrt{A{B}^{2}+B{C}^{2}}$=4$\sqrt{3}$�����ε����Ϊs=12$\sqrt{3}$����������Բ��İ뾶Ϊr=2$\sqrt{3}$��
����������ʽ�ɵã�4��R2=64�У����R=4�����ĵ�����ľ���Ϊd=$\sqrt{{R}^{2}-{r}^{2}}$=2��
����O-ABCD�����Ϊ$\frac{1}{3}$d•s=$\frac{1}{3}$��2��12$\sqrt{3}$=8$\sqrt{3}$���ʢ۲���ȷ��
�ܣ���������ABCD-A1B1C1D1�Ͻ�����ͼ��ʾ�ռ�ֱ������ϵ��
�������������ⳤΪ1������B1D������B1D����ȡһ��P��
��Ϊ$\overrightarrow{D{B}_{1}}$=��1��1��1����������P��a��a��a��������0��a��1��
��PE��ƽ��A1D������ΪE������EF��A1D1������ΪF��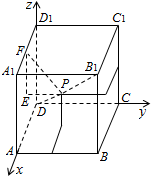
��PF�ǵ�P��ֱ��A1D1�ľ��룮
����PF=$\sqrt{{a}^{2}+��1-a��^{2}}$��
ͬ����P��ֱ��AB��CC1�ľ���Ҳ��$\sqrt{{a}^{2}+��1-a��^{2}}$��
����B1D����һ����������ABCD-A1B1C1D1��������AB��CC1��A1D1����ֱ�ߵľ��붼��ȣ�
������������ABCD-A1B1C1D1��������AB��CC1��A1D1����ֱ�ߵľ�����ȵĵ������������ʢܲ���ȷ��
�ʴ�Ϊ���٢ڣ�
���� ���⿼�����������жϣ���Ҫ�ǿռ���ֱ�ߵ�λ�ù�ϵ��ƽ��������塢��Ľ������ʺ�����������������еĵ�����ľ��룬ע�����þٷ�����ֱ�ӷ��ͽ����ռ�ֱ������ϵ�������жϺ��������ռ�������������������������һ�����ۺ��ԣ�


 ���㼤�������100�ִ��Ծ�ϵ�д�
���㼤�������100�ִ��Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 2 | C�� | 1 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [$\frac{2}{5{e}^{2}}$��$\frac{1}{3e}$�� | B�� | [$\frac{1}{3e}$��$\frac{\sqrt{e}}{4e}$�� | C�� | [$\frac{1}{3e}$��e] | D�� | [$\frac{\sqrt{e}}{4e}$��e] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $��1��\frac{{\sqrt{6}}}{2}]$ | B�� | $[\frac{{\sqrt{6}}}{2}��+�ޣ�$ | C�� | $��1��\frac{{\sqrt{6}}}{2}��$ | D�� | $��\frac{{\sqrt{6}}}{2}��+�ޣ�$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com