
【题目】甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲 | 82 | 81 | 79 | 78 | 95 | 88 | 93 | 84 |
乙 | 92 | 95 | 80 | 75 | 83 | 80 | 90 | 85 |
(1)用茎叶图表示这两组数据;
(2)现要从中选派一人参加数学竞赛,从统计学的角度(在平均数、方差或标准差中选两个)考虑,你认为选派哪位学生参加合适?请说明理由.
【答案】
(1)解:茎叶图如下:

(2)解:派甲参加比较合适,理由如下:
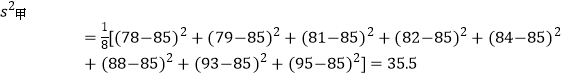
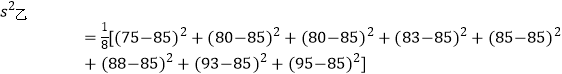 (90﹣85)2+(92﹣85)2+(95﹣85)2]=41
(90﹣85)2+(92﹣85)2+(95﹣85)2]=41
∵ ![]() =
= ![]() ,
, ![]() ,
,
∴甲的成绩较稳定,派甲参赛比较合适
【解析】(1)将成绩的十位数作为茎,个位数作为叶,可得茎叶图;(2)计算甲与乙的平均数与方差,即可求得结论.
【考点精析】认真审题,首先需要了解茎叶图(茎叶图又称“枝叶图”,它的思路是将数组中的数按位数进行比较,将数的大小基本不变或变化不大的位作为一个主干(茎),将变化大的位的数作为分枝(叶),列在主干的后面,这样就可以清楚地看到每个主干后面的几个数,每个数具体是多少),还要掌握平均数、中位数、众数(⑴平均数、众数和中位数都是描述一组数据集中趋势的量;⑵平均数、众数和中位数都有单位;⑶平均数反映一组数据的平均水平,与这组数据中的每个数都有关系,所以最为重要,应用最广;⑷中位数不受个别偏大或偏小数据的影响;⑸众数与各组数据出现的频数有关,不受个别数据的影响,有时是我们最为关心的数据)的相关知识才是答题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2 ![]() sinxcosx+1﹣2sin2x,x∈R.
sinxcosx+1﹣2sin2x,x∈R.
(1)求函数f(x)的最小正周期和单调递增区间;
(2)将函数y=f(x)的图象上各点的纵坐标保持不变,横坐标缩短到原来的 ![]() ,把所得到的图象再向左平移
,把所得到的图象再向左平移 ![]() 单位,得到的函数y=g(x)的图象,求函数y=g(x)在区间
单位,得到的函数y=g(x)的图象,求函数y=g(x)在区间 ![]() 上的最小值.
上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin(x+ ![]() )cosx.
)cosx.
(Ⅰ)求f(x)的值域;
(Ⅱ)设△ABC的内角A、B、C所对的边分别为a、b、c,已知A为锐角,f(A)= ![]() ,b=2,c=3,求cos(A﹣B)的值.
,b=2,c=3,求cos(A﹣B)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(1),五边形![]() 中,
中, ![]() .如图(2),将
.如图(2),将![]() 沿
沿![]() 折到
折到![]() 的位置,得到四棱锥
的位置,得到四棱锥![]() .点
.点![]() 为线段
为线段![]() 的中点,且
的中点,且![]() 平面
平面![]() .
.
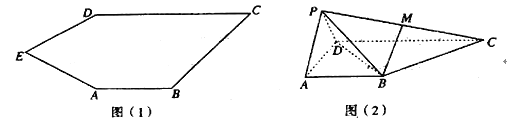
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若直线![]() 与
与![]() 所成角的正切值为
所成角的正切值为![]() ,设
,设![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,直线
,直线![]() 被椭圆
被椭圆![]() 截得的线段长为
截得的线段长为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过原点的直线与椭圆![]() 交于
交于![]() ,
, ![]() 两点(
两点(![]() ,
, ![]() 不是椭圆
不是椭圆![]() 的顶点),点
的顶点),点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() .直线
.直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 两点.设直线
两点.设直线![]() 的斜率分别为
的斜率分别为![]() ,证明存在常数
,证明存在常数![]() 使得
使得![]() ,并求出
,并求出![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]()
![]() ,其中
,其中 ![]() =(2cosx,﹣
=(2cosx,﹣ ![]() sin2x),
sin2x), ![]() =(cosx,1),x∈R
=(cosx,1),x∈R
(Ⅰ)求函数y=f(x)的单调递减区间;
(Ⅱ)在△ABC中,角A,B,C所对的边分别为a,b,c,f(A)=﹣1,a= ![]() ,且向量
,且向量 ![]() =(3,sinB)与向量
=(3,sinB)与向量 ![]() =(2,sinC)共线,求△ABC的面积.
=(2,sinC)共线,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是根据部分城市某年6月份的平均气温(单位:℃)数据得到的样本频率分布直方图,其中平均气温的范围是[20.5,26.5].已知样本中平均气温不大于22.5℃的城市个数为11,则样本中平均气温不低于25.5℃的城市个数为 . 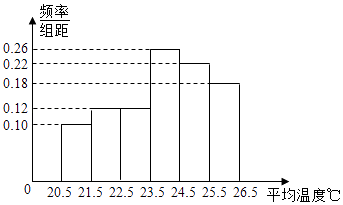
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com