
| A. | [-2,2] | B. | [-∞,-2]∪[2,+∞) | C. | [-2$\sqrt{2}$,2$\sqrt{2}$] | D. | (-∞,-2$\sqrt{2}$]∪[2$\sqrt{2}$,+∞) |
分析 由直线mx+ny=2与圆x2+y2=1相切,得m2+n2=4,从而mn≤$\frac{{m}^{2}+{n}^{2}}{2}$=2,进而(m+n)2=m2+n2+2mn≤4+2×2=8,由此能求出m+n的取值范围.
解答 解:∵m,n∈R,直线mx+ny=2与圆x2+y2=1相切,
∴圆心(0,0)到直线的距离d=$\frac{|0+0-2|}{\sqrt{{m}^{2}+{n}^{2}}}$=1,
解得m2+n2=4,
∴mn≤$\frac{{m}^{2}+{n}^{2}}{2}$=2,
∴(m+n)2=m2+n2+2mn≤4+2×2=8,
∴-2$\sqrt{2}≤m+n≤2\sqrt{2}$.
∴m+n的取值范围是[-2$\sqrt{2}$,2$\sqrt{2}$].
故选:C.
点评 本题考查代数和取值范围的求法,考查直线方程、圆、点到直线的距离公式、基本不等式等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.


科目:高中数学 来源:2017届山西临汾一中高三10月月考数学(理)试卷(解析版) 题型:解答题
如图, 在四棱锥 中,
中, 底面
底面 ,底面
,底面 是直角梯形,
是直角梯形,
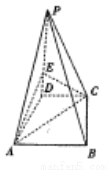
(1)在 上确定一点
上确定一点 ,使得
,使得 平面
平面 ,并求
,并求 的值;
的值;
(2)在(1)条件下, 求平面 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源:2017届重庆市高三10月月考数学(文)试卷(解析版) 题型:选择题
(改编)已知复数 ,则复数
,则复数 在复平面上对应的点位于( )
在复平面上对应的点位于( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知正方形ABCD与矩形ACEF所在的平面互相垂直,AB=2,AF=1.
如图,已知正方形ABCD与矩形ACEF所在的平面互相垂直,AB=2,AF=1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在凸四边形ABCD中,AB=1,BC=$\sqrt{3}$,AC⊥CD,AC=CD.当∠ABC=45°时,对角线BD的长为$\sqrt{7}$.
如图,在凸四边形ABCD中,AB=1,BC=$\sqrt{3}$,AC⊥CD,AC=CD.当∠ABC=45°时,对角线BD的长为$\sqrt{7}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图是正方体的平面展开图,在这个正方体中,
如图是正方体的平面展开图,在这个正方体中,| A. | ③ | B. | ③④ | C. | ①③ | D. | ①③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(cosA)>f(sinB) | B. | f(sinA)>f(cosB) | C. | f(cosA)≥f(sinB) | D. | f(sinA)≥f(cosB) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AD}$ | B. | $\frac{1}{4}$$\overrightarrow{AB}$+$\frac{3}{4}$$\overrightarrow{AD}$ | C. | $\frac{1}{5}$$\overrightarrow{AB}$+$\frac{4}{5}$$\overrightarrow{AD}$ | D. | $\frac{2}{5}$$\overrightarrow{AB}$+$\frac{3}{5}$$\overrightarrow{AD}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com