
(本题满分18分)在平面直角坐标系中,已知动点 ,点
,点 点
点 与点
与点 关于直线
关于直线 对称,且
对称,且 .直线
.直线 是过点
是过点 的任意一条直线.
的任意一条直线.
(1)求动点 所在曲线
所在曲线 的轨迹方程;
的轨迹方程;
(2)设直线 与曲线
与曲线 交于
交于 两点,且
两点,且 ,求直线
,求直线 的方程;
的方程;
(3)若直线 与曲线
与曲线 交于
交于 两点,与线段
两点,与线段 交于点
交于点 (点
(点 不同于点
不同于点 ),直线
),直线 与直线
与直线 交于点
交于点 ,求证:
,求证: 是定值.
是定值.
(1) 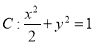 ; (2)
; (2) 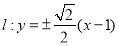 ; (3)定值为1;证明祥见解析.
; (3)定值为1;证明祥见解析.
【解析】
试题分析:(1)求出N的坐标,运用向量的数量积的坐标表示,化简即可得到轨迹方程;
(2)设l:y=k(x-1),联立椭圆方程,消去y,运用韦达定理和弦长公式,即可求得斜率,进而得到直线方程;
(3)求出HA,GB的方程,设出Q的坐标,由(2)得,P(0,-k),再由直线GB与直线HA交于点O,解得Q的纵坐标,再由向量的数量积的坐标表示,即可得到定值1.
试题解析:(1)依据题意,可得点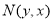 .
.
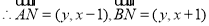 .
.
又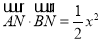 ,
,
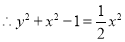 .
.
 所求动点
所求动点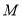 的轨迹方程为
的轨迹方程为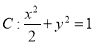 .
.
(2)若直线 轴,则可求得
轴,则可求得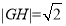 ,这与已知矛盾,因此满足题意的直线
,这与已知矛盾,因此满足题意的直线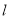 不平行于
不平行于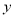 轴.
轴.
设直线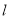 的斜率为
的斜率为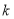 ,则
,则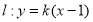 .
.
由 得
得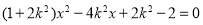 .
.
设点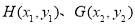 ,有
,有 且
且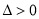 恒成立(因点
恒成立(因点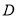 在椭圆内部).
在椭圆内部).
又 ,
,
于是,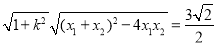 ,即
,即 ,
,
解得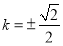 .
.
所以,所求直线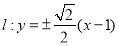 .
.
证明(3)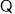 直线
直线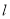 与线段
与线段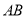 交于点
交于点 ,且与点
,且与点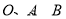 不重合,
不重合,
 直线
直线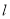 的斜率
的斜率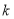 满足:
满足: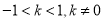 .
.
由(2)可得点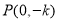 ,
,
可算得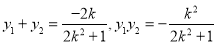 .
.
又直线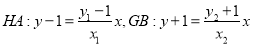 .
.
设点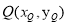 ,则由
,则由 得
得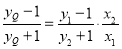 (此等式右边为正数).
(此等式右边为正数).

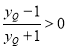 ,且
,且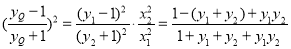 =
=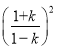 .
.

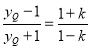 ,解得
,解得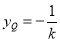 .
.
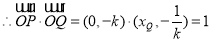 为定值.
为定值.
考点:直线与圆锥曲线的综合问题.


科目:高中数学 来源:[同步]2014年北师大版选修2-1 2.1从平面向量到空间向量练习卷(解析版) 题型:选择题
已知{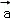 ,
,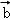 ,
,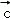 }是空间的一组单位正交基底,而{
}是空间的一组单位正交基底,而{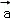 ﹣
﹣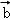 ,
,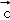 ,
, +
+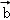 }是空间的另一组基底.若向量
}是空间的另一组基底.若向量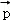 在基底{
在基底{ ,
,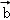 ,
,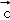 }下的坐标为(6,4,2),则向量
}下的坐标为(6,4,2),则向量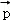 在基底{
在基底{ ﹣
﹣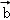 ,
,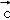 ,
,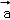 +
+ }下的坐标为( )
}下的坐标为( )
A.(1,2,5) B.(5,2,1) C.(1,2,3) D.(3,2,1)
查看答案和解析>>
科目:高中数学 来源:2014-2015学年四川省成都市高三第一次诊断性检测理科数学试卷(解析版) 题型:选择题
若关于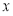 的方程
的方程 在区间
在区间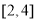 上有实数根,则实数
上有实数根,则实数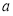 的取值范围是( )
的取值范围是( )
(A)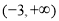 (B)
(B)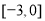 (C)
(C)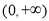 (D)
(D)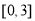
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上海市黄浦区高三上学期期终调研测试文科数学试卷(解析版) 题型:填空题
一副扑克牌(有四色,同一色有13张不同牌)共52张.现随机抽取3张牌,则抽出的3张牌有且仅有2张花色相同的概率为 (用数值作答).
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上海市黄浦区高三上学期期终调研测试文科数学试卷(解析版) 题型:填空题
已知抛物线 的顶点在坐标原点,焦点与双曲线:
的顶点在坐标原点,焦点与双曲线: 的右焦点重合,则抛物线
的右焦点重合,则抛物线 的方程是 .
的方程是 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上海市黄浦区高三上学期期终调研测试理科数学试卷(解析版) 题型:选择题
已知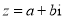
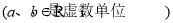 ,
,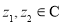 ,定义:
,定义: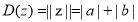 ,
,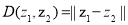 .给出下列命题:
.给出下列命题:
(1)对任意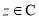 ,都有
,都有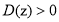 ;
;
(2)若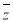 是复数
是复数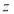 的共轭复数,则
的共轭复数,则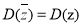 恒成立;
恒成立;
(3)若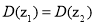
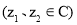 ,则
,则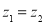 ;
;
(4)对任意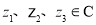 ,结论
,结论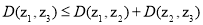 恒成立,则其中真命题是[答]( ).
恒成立,则其中真命题是[答]( ).
A.(1)(2)(3)(4) B.(2)(3)(4) C.(2)(4) D.(2)(3)
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上海市黄浦区高三上学期期终调研测试理科数学试卷(解析版) 题型:填空题
已知 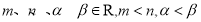 ,若
,若 是函数
是函数 的零点,则
的零点,则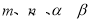 四个数按从小到大的顺序是 (用符号
四个数按从小到大的顺序是 (用符号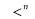 连接起来).
连接起来).
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河北省邯郸市高三上学期1月份教学质量检测文科数学试卷(解析版) 题型:选择题
执行如图所示的程序框图,若输入的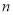 值等于7,则输出的
值等于7,则输出的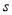 的值为( )
的值为( )
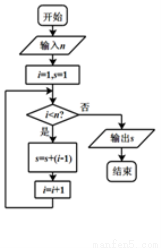
A.15 B.16 C.21 D.22
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com