
分析 (1)设AB与x轴交于点R,求出|AR|,|CR|,即可求抛物线E的方程;
(2)求出圆D,C的方程,两圆相减,可得直线PQ的方程,利用直线PQ经过点O,即可求点N的坐标及|PQ|长度.
解答 解:(1)由已知得M(-$\frac{p}{2}$,0),C(2,0).
设AB与x轴交于点R,
由圆的对称性可知,|AR|=$\frac{2\sqrt{2}}{3}$.
于是|CR|=$\frac{1}{3}$
所以|CM|=$\frac{|AC|}{sin∠AMC}$=$\frac{|AC|}{sin∠CAR}$=3,
即2+$\frac{p}{2}$=3,p=2.
故抛物线E的方程为y2=4x.
(2)设N(s,t).
P,Q是NC为直径的圆D与圆C的两交点.
圆D方程为(x-$\frac{s+2}{2}$)2+(y-$\frac{t}{2}$)2=$\frac{(s-2)^{2}+{t}^{2}}{4}$,
即x2+y2-(s+2)x-ty+2s=0.①
又圆C方程为x2+y2-4x+3=0.②
②-①得(s-2)x+ty+3-2s=0.③
P,Q两点坐标是方程①和②的解,也是方程③的解,从而③为直线PQ的方程.
因为直线PQ经过点O,所以3-2s=0,s=$\frac{3}{2}$.
故点N坐标为($\frac{3}{2}$,$±\sqrt{6}$),
PQ的方程为-$\frac{1}{2}$x$±\sqrt{6}$y=0,|PQ|=$\frac{2\sqrt{21}}{5}$.
点评 本题考查抛物线的方程,考查圆的方程,考查两圆的位置关系,考查学生分析解决问题的能力,求得PQ的方程是关键.


科目:高中数学 来源: 题型:解答题
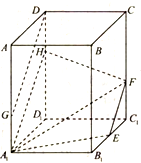 在正四棱柱ABCD-A1B1C1D1中,AB=2,AA1=3,E为B1C1的中点,F在CC1上,且C1F=1,G在AA1上,且AG=2.
在正四棱柱ABCD-A1B1C1D1中,AB=2,AA1=3,E为B1C1的中点,F在CC1上,且C1F=1,G在AA1上,且AG=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(2a)<f(2)<f(log2a) | B. | f(2)<f(2a)<f(log2a) | C. | f(log2a)<f(2a)<f(2) | D. | f(2)<f(log2a)<f(2a) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | $\sqrt{2}$或1 | D. | 2$\sqrt{2}$或$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\frac{{3\sqrt{2}}}{2}$ | C. | $2\sqrt{2}$ | D. | $\frac{{5\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com