
分析 (1)由题意得$\sqrt{3}b=a$,根据椭圆短轴的一个端点与两个焦点构成的三角形的面积为$\frac{{5\sqrt{2}}}{3}$,可得$\frac{1}{2}×b×2c=\frac{{5\sqrt{2}}}{3}$,再结合隐含条件求得a2,b2的值,则椭圆方程可求;
(2)①联立直线方程和椭圆方程,利用根与系数的关系可得线段AB的中点的横坐标,由线段AB的中点的横坐标为$-\frac{1}{2}$列式求得k值;②由(2)①中根与系数的关系及平面向量的坐标运算求得$\overrightarrow{MA}•\overrightarrow{MB}$为定值$\frac{4}{9}$.
解答 (1)解:∵椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$满足a2=b2+c2,$\sqrt{3}b=a$,
根据椭圆短轴的一个端点与两个焦点构成的三角形的面积为$\frac{{5\sqrt{2}}}{3}$,
可得$\frac{1}{2}×b×2c=\frac{{5\sqrt{2}}}{3}$.
从而可解得${a^2}=5,\;\;{b^2}=\frac{5}{3}$,
∴椭圆C的标准方程为$\frac{x^2}{5}+\frac{y^2}{{\frac{5}{3}}}=1$;
(2)①解:设A(x1,y1),B(x2,y2),
将y=k(x+1)代入$\frac{x^2}{5}+\frac{y^2}{{\frac{5}{3}}}=1$中,
消元得(1+3k2)x2+6k2x+3k2-5=0,
△=36k4-4(3k2+1)(3k2-5)=48k2+20>0,
${x_1}+{x_2}=-\frac{{6{k^2}}}{{3{k^2}+1}}$,
∵AB中点的横坐标为$-\frac{1}{2}$,∴$-\frac{{3{k^2}}}{{3{k^2}+1}}=-\frac{1}{2}$,解得$k=±\frac{{\sqrt{3}}}{3}$;
②证明:由①知${x_1}+{x_2}=-\frac{{6{k^2}}}{{3{k^2}+1}}$,${x_1}{x_2}=\frac{{3{k^2}-5}}{{3{k^2}+1}}$,
∴$\overrightarrow{MA}\;•\;\overrightarrow{MB}=({{x_1}+\frac{7}{3},\;\;{y_1}})\;•\;({{x_2}+\frac{7}{3},\;\;{y_2}})=({{x_1}+\frac{7}{3}})\;•\;({{x_2}+\frac{7}{3}})+{y_1}{y_2}$
=$({{x_1}+\frac{7}{3}})\;•\;({{x_2}+\frac{7}{3}})+{k^2}({x_1}+1)({x_2}+1)$=$(1+{k^2}){x_1}{x_2}+({\frac{7}{3}+{k^2}})({x_1}+{x_2})+\frac{49}{9}+{k^2}$
=$(1+{k^2})\frac{{3{k^2}-5}}{{3{k^2}+1}}+({\frac{7}{3}+{k^2}})({-\frac{{6{k^2}}}{{3{k^2}+1}}})+\frac{49}{9}+{k^2}$=$\frac{{-3{k^4}-16{k^2}-5}}{{3{k^2}+1}}+\frac{49}{9}+{k^2}=\frac{4}{9}$.
点评 本题考查椭圆的简单性质,考查了直线与椭圆位置关系的应用,考查平面向量的数量积运算,体现了“设而不求”的解题思想方法,是中档题.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | g(x)的图象关于直线$x=\frac{π}{2}$对称 | B. | g(x)的图象关于点(π,0)对称 | ||
| C. | g(x)在$[0,\frac{π}{2}]$上递增 | D. | g(x)在[0,π]上递减 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
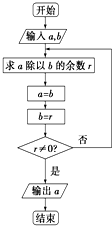 我国古代名著《九章算术》用“更相减损术”求两个正整数的最大公约数是一个伟大的创举,这个伟大创举与古老的算法--“辗转相除法”实质一样,如图的程序框图源于“辗转相除法”.当输入a=6102,b=2016时,输出的a=( )
我国古代名著《九章算术》用“更相减损术”求两个正整数的最大公约数是一个伟大的创举,这个伟大创举与古老的算法--“辗转相除法”实质一样,如图的程序框图源于“辗转相除法”.当输入a=6102,b=2016时,输出的a=( )| A. | 6 | B. | 9 | C. | 12 | D. | 18 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com