Question

15．如图，三棱锥C-ABD中，C是以AB为直径的半圆上一点，点E在直径AB上，已知AB=10，AC=2$\sqrt{5}$，CE=4，CD=3$\sqrt{2}$，AD=DE=$\sqrt{2}$．
（1）求证：CE⊥平面ABD；
（2）求直线BC与平面ACD所成角的正弦值．

Answer 1

分析 （1）只要证明CE⊥AB，CE⊥ED，利用线面垂直的判定定理可证；
（2）利用V_B-ACD=V_D-ABC，求出平面ACD上的高即可．

解答 证明：（1）∵$\frac{CE}{CA}$=$\frac{4}{2\sqrt{5}}$=$\frac{BC}{AB}$=$\frac{\sqrt{A{B}^{2}-A{C}^{2}}}{AB}$=$\frac{\sqrt{80}}{10}$，
∴△ABC∽△BCE，∠ACB=∠BEC=90°，可得CE⊥AB，
∵△ECD中，CE²+ED²=16+2=18=CD²，由勾股定理的逆定理可得：CE⊥ED
∵AB∩ED=E，
∴CE⊥平面ABD；
解：（2）设B到平面ACD的距离为h，由V_B-ACD=V_D-ABC，
其中，在△ACD中，AC²=20=AD²+CD²=2+18，∴AD⊥CD，故△ADE是等腰直角三角形，AD=DE=$\sqrt{2}$，∴棱锥底面ABC上的高为DF=1，如图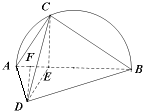
∴${V}_{D-ABC}=\frac{1}{3}×\frac{1}{2}×AC×BC×DF$=$\frac{1}{3}×\frac{1}{2}×2\sqrt{5}×\sqrt{A{B}^{2}-A{C}^{2}}×1$=$\frac{20}{3}$，
${V}_{B-ACD}=\frac{1}{3}×\frac{1}{2}×AD×CD×h$=$\frac{1}{6}×\sqrt{2}×3\sqrt{2}h$=h，
∴h=$\frac{20}{3}$，
∴直线BC与平面ACD所成角的正弦值为：$\frac{h}{BC}=\frac{\frac{20}{3}}{4\sqrt{5}}=\frac{\sqrt{5}}{3}$．

点评 本题考查了线面垂直的判定定理的运用以及线面角的求法；关键是将问题转化为线线关系问题解答．