
分析 对任意n∈N*,${a_{n+1}}={a_n}^2+{a_n}$,可得$\frac{1}{{a}_{n+1}}$=$\frac{1}{{a}_{n}({a}_{n}+1)}$,可得:$\frac{1}{{a}_{n+1}}$-$\frac{1}{{a}_{n}}$=-$\frac{1}{{a}_{n}+1}$,于是$\sum_{n=1}^{2016}{\frac{1}{{{a_n}+1}}}$=$\frac{1}{{a}_{1}}$-$\frac{1}{{a}_{2017}}$=3-$\frac{1}{{a}_{2017}}$.由${a}_{1}=\frac{1}{3}$,a2<1,a3<1,a4>1,可得n≥4时,$\frac{1}{{a}_{n}}$∈(0,1),即可得出.
解答 解:∵对任意n∈N*,${a_{n+1}}={a_n}^2+{a_n}$,
∴$\frac{1}{{a}_{n+1}}$=$\frac{1}{{a}_{n}({a}_{n}+1)}$,可得:$\frac{1}{{a}_{n+1}}$-$\frac{1}{{a}_{n}}$=-$\frac{1}{{a}_{n}+1}$,
∴$\sum_{n=1}^{2016}{\frac{1}{{{a_n}+1}}}$=-$(\frac{1}{{a}_{2017}}-\frac{1}{{a}_{2016}})$-$(\frac{1}{{a}_{2016}}-\frac{1}{{a}_{2015}})$-…-$(\frac{1}{{a}_{2}}-\frac{1}{{a}_{1}})$
=$\frac{1}{{a}_{1}}$-$\frac{1}{{a}_{2017}}$=3-$\frac{1}{{a}_{2017}}$.
∵a2=$(\frac{1}{3})^{2}+\frac{1}{3}$=$\frac{4}{9}$,a3=$(\frac{4}{9})^{2}+\frac{4}{9}$=$\frac{52}{81}$,a4=$(\frac{52}{81})^{2}+\frac{52}{81}$=$\frac{6916}{6561}$>1,
∴n≥4时,$\frac{1}{{a}_{n}}$∈(0,1),
∴3-$\frac{1}{{a}_{2017}}$∈(2,3).
∴$\sum_{n=1}^{2016}{\frac{1}{{{a_n}+1}}}$的整数部分是2.
故答案为:2.
点评 本题考查了数列递推关系、“裂项求和”方法、整数的性质,考查了推理能力与计算能力,属于中档题.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{20}$ | B. | $\frac{1}{5}$ | C. | $\frac{3}{10}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3对 | B. | 2对 | C. | 1对 | D. | 0对 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
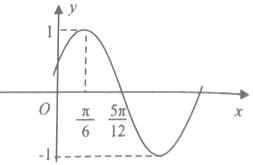 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com