
分析 根据向量的加减的几何意义以及,向量的模的计算,设AC=x,构造方程,求出x,再根据向量的数量积公式计算即可.
解答 解:$\overrightarrow{AD}$=$\overrightarrow{AB}$+$\overrightarrow{BD}$=$\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{BC}$=$\overrightarrow{AB}$+$\frac{1}{3}$($\overrightarrow{AC}$-$\overrightarrow{AB}$)=$\frac{2}{3}$$\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{AC}$,
∵AD=$\frac{\sqrt{37}}{3}$,设AC=x,
∴$\frac{4}{9}$${\overrightarrow{AB}}^{2}$+$\frac{4}{9}$$\overrightarrow{AB}•\overrightarrow{AC}$+$\frac{1}{9}$${\overrightarrow{AC}}^{2}$=$\frac{37}{9}$,
∴$\frac{16}{9}$+$\frac{4}{9}$×2xcos60°+$\frac{{x}^{\;}}{9}$=$\frac{37}{9}$,
∴x2+4x-21=0,
解得x=3,x=-7(舍去),
∴$\overrightarrow{AB}•\overrightarrow{AC}$=2×3×$\frac{1}{2}$=3,
故答案为:3
点评 本题考查了向量的数量积的运算和向量模的计算,属于中档题.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
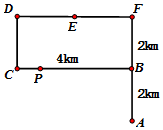 8月27日我校组织了高一学生拉练活动,步行路线如图:A→B→C→D→E→F→A(A是学校,BCDF为矩形,AB=BF=2km,BC=4km),步行匀速前进,速度4km/h,拉练过程中在DF的中点E处休息了半小时,从学校A点出发开始计时,经过t小时到达P点,P到A的直线距离为|PA|,设y=|PA|2.
8月27日我校组织了高一学生拉练活动,步行路线如图:A→B→C→D→E→F→A(A是学校,BCDF为矩形,AB=BF=2km,BC=4km),步行匀速前进,速度4km/h,拉练过程中在DF的中点E处休息了半小时,从学校A点出发开始计时,经过t小时到达P点,P到A的直线距离为|PA|,设y=|PA|2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $-\frac{8}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{8}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x+1)是偶函数 | B. | f(x+1)是非奇非偶函数 | ||
| C. | f(x)=f(x+2) | D. | f(x+3)是奇函数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com