
分析 (1)求得g(x)的解析式和导数,可得切线的斜率和切点,由点斜式方程,可得切线的方程;
(2)先求出f(x)的导函数,然后求出导函数的根,讨论a的取值范围分别求出函数的单调增区间,使(0,2)是增区间的子集即可,解不等式即可得到所求a的范围.
解答 解:(1)函数g(x)=f(x)-b=-x3+x2,
导数为g′(x)=-3x2+2x,
函数g(x)在(1,g(1))处的切线斜率为-3+2=-1,
切点为(1,0),可得切线的方程为y=-(x-1),
即x+y-1=0;
(2)由题意,得f'(x)=-3x2+2ax,
令f′(x)=0,解得x=0或x=$\frac{2}{3}$a,
当a<0时,由f′(x)>0,解得$\frac{2a}{3}$<x<0,
所以f(x)在($\frac{2a}{3}$,0)上是增函数,与题意不符,舍去;
当a=0时,由f'(x)=-3x2≤0,与题意不符,舍去;
当a>0时,由f′(x)>0,解得0<x<$\frac{2a}{3}$,
所以f(x)在(0,$\frac{2a}{3}$)上是增函数,
又f(x)在(0,2)上是增函数,
所以$\frac{2a}{3}$≥2,解得a≥3,
综上,a的取值范围为[3,+∞).
点评 本题主要考查了利用导数研究函数的单调性,以及转化思想和分类讨论的综合运用,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
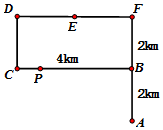 8月27日我校组织了高一学生拉练活动,步行路线如图:A→B→C→D→E→F→A(A是学校,BCDF为矩形,AB=BF=2km,BC=4km),步行匀速前进,速度4km/h,拉练过程中在DF的中点E处休息了半小时,从学校A点出发开始计时,经过t小时到达P点,P到A的直线距离为|PA|,设y=|PA|2.
8月27日我校组织了高一学生拉练活动,步行路线如图:A→B→C→D→E→F→A(A是学校,BCDF为矩形,AB=BF=2km,BC=4km),步行匀速前进,速度4km/h,拉练过程中在DF的中点E处休息了半小时,从学校A点出发开始计时,经过t小时到达P点,P到A的直线距离为|PA|,设y=|PA|2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{12}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com