
分析 先根据二倍角公式化简,再根据基本不等式即可求出答案.
解答 解:$f(x)=\frac{9}{8cos2x+16}-{sin^2}x$=$\frac{9}{8cos2x+16}$+$\frac{cos2x-1}{2}$
=$\frac{\frac{9}{8}}{cos2x+2}$+$\frac{cos2x+2}{2}$-$\frac{3}{2}$,
∵cos2x+2>0,
∴f(x)≥2×$\frac{3}{4}$-$\frac{3}{2}$=0,当且仅当$\frac{\frac{9}{8}}{cos2x+2}$=$\frac{cos2x+2}{2}$,
即cos2x=-$\frac{1}{2}$时等号成立,则x的最小正值为n=$\frac{π}{3}$,
∴m+n=$\frac{π}{3}$.
故答案为:$\frac{π}{3}$
点评 本题考查了三角函数的化简和基本不等式的应用,属于中档题.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
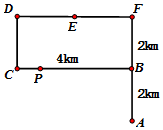 8月27日我校组织了高一学生拉练活动,步行路线如图:A→B→C→D→E→F→A(A是学校,BCDF为矩形,AB=BF=2km,BC=4km),步行匀速前进,速度4km/h,拉练过程中在DF的中点E处休息了半小时,从学校A点出发开始计时,经过t小时到达P点,P到A的直线距离为|PA|,设y=|PA|2.
8月27日我校组织了高一学生拉练活动,步行路线如图:A→B→C→D→E→F→A(A是学校,BCDF为矩形,AB=BF=2km,BC=4km),步行匀速前进,速度4km/h,拉练过程中在DF的中点E处休息了半小时,从学校A点出发开始计时,经过t小时到达P点,P到A的直线距离为|PA|,设y=|PA|2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 相离 | B. | 相切 | C. | 相交且不过圆心 | D. | 相交且过圆心 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com