分析法又称执果索因法，若用分析法证明：“设a＞b＞c，且a+b+c=0”，求证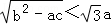
”索的因应是（ ）
A.a﹣b＞0
B.a﹣c＞0
C.（a﹣b）（a﹣c）＞0
D.（a﹣b）（a﹣c）＜0
科目：高中数学 来源：[同步]2014年新人教A版选修4-1 3.1平行射影练习卷（解析版） 题型：填空题
给出下列四个命题：
①设x1，x2∈R，则x1＞1且x2＞1的充要条件是x1+x2＞2且x1x2＞1；
②任意的锐角三角形ABC中，有sinA＞cosB成立；
③平面上n个圆最多将平面分成2n2﹣4n+4个部分；
④空间中直角在一个平面上的正投影可以是钝角．
其中真命题的序号是 （要求写出所有真命题的序号）．
查看答案和解析>>
科目：高中数学 来源：[同步]2014年新人教A版选修4-1 2.1圆周角定理练习卷（解析版） 题型：填空题
（2013•惠州二模）（几何证明选讲选做题）
如图所示，AB是圆O的直径，
，AB=10，BD=8，则cos∠BCE= ．
查看答案和解析>>
科目：高中数学 来源：[同步]2014年北师大版选修1-2 3.3综合法与分析法练习卷（解析版） 题型：选择题
“π是无限不循环小数，所以π是无理数”，以上推理（ ）
A.缺少小前提，小前提是无理数都是无限不循环小数
B.缺少大前提，大前提是无理数都是无限不循环小数
C.缺少小前提，小前提是无限不循环小数都是无理数
D.缺少大前提，大前提是无限不循环小数都是无理数
查看答案和解析>>
科目：高中数学 来源：[同步]2014年北师大版选修1-2 3.3综合法与分析法练习卷（解析版） 题型：选择题
设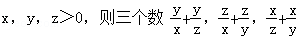
（ ）
A.都大于2
B.至少有一个大于2
C.至少有一个不小于2
D.至少有一个不大于2
查看答案和解析>>
科目：高中数学 来源：[同步]2014年北师大版选修1-2 3.3综合法与分析法练习卷（解析版） 题型：选择题
（2014•合肥一模）对于函数f（x），若?a，b，c∈R，f（a），f（b），f（c）都是某一三角形的三边长，则称f（x）为“可构造三角形函数”．以下说法正确的是（ ）
A.f（x）=1（x∈R）不是“可构造三角形函数”
B.“可构造三角形函数”一定是单调函数
C.f（x）=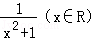
是“可构造三角形函数”
D.若定义在R上的函数f（x）的值域是
（e为自然对数的底数），则f（x）一定是“可构造三角形函数”
查看答案和解析>>
科目：高中数学 来源：[同步]2014年北师大版选修1-2 3.2数学证明练习卷（解析版） 题型：选择题
（2014•天津一模）定义一种新运算：a?b=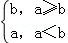
，已知函数f（x）=（1+
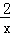）?3log2（x+1），若方程f（x）﹣k=0恰有两个不相等的实根，则实数k的取值范围为（ ）
A.（﹣∞，3）
B.（1，3）
C.（﹣∞，﹣3）∪（1，3）
D.（﹣∞，﹣3）∪（0，3）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
＜
a，经过分析，只要证（a﹣c）（a﹣b）＞0，从而得出结论．
＜
