
【题目】已知椭圆![]() 的一个焦点与抛物线
的一个焦点与抛物线![]() 的焦点重合,且此抛物线的准线被椭圆
的焦点重合,且此抛物线的准线被椭圆![]() 截得的弦长为
截得的弦长为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,直线
,直线![]() 是线段
是线段![]() 的垂直平分线,试问直线
的垂直平分线,试问直线![]() 是否过定点?若是,请求出该定点的坐标;若不是,请说明理由.
是否过定点?若是,请求出该定点的坐标;若不是,请说明理由.
【答案】(1)![]() ;(2)直线
;(2)直线![]() 过定点
过定点![]() ,详见解析.
,详见解析.
【解析】
(1)由题意得出![]() ,由题意知点
,由题意知点![]() 在椭圆
在椭圆![]() 上,由此得出关于
上,由此得出关于![]() 、
、![]() 的方程组,求出
的方程组,求出![]() 、
、![]() 的值,即可得出椭圆
的值,即可得出椭圆![]() 的标准方程;
的标准方程;
(2)解法一:由题意可知,直线![]() 的斜率不为零,然后分直线
的斜率不为零,然后分直线![]() 的斜率存在且不为零和直线
的斜率存在且不为零和直线![]() 的斜率不存在两种情况讨论,在第一种情况下,设直线
的斜率不存在两种情况讨论,在第一种情况下,设直线![]() 的方程为
的方程为![]() ,设点
,设点![]() 、
、![]() ,将直线
,将直线![]() 的方程与椭圆
的方程与椭圆![]() 的方程联立,列出韦达定理,由
的方程联立,列出韦达定理,由![]() 得出
得出![]() ,并写出直线
,并写出直线![]() 的方程,由此可得出直线
的方程,由此可得出直线![]() 所过定点的坐标;在第二种情况下可得出直线
所过定点的坐标;在第二种情况下可得出直线![]() 为
为![]() 轴,即可得出直线
轴,即可得出直线![]() 过定点
过定点![]() ,由此得出结论;
,由此得出结论;
解法二:由题意可知,直线![]() 的斜率不为零,然后分直线
的斜率不为零,然后分直线![]() 的斜率存在且不为零和直线
的斜率存在且不为零和直线![]() 的斜率不存在两种情况讨论,在第一种情况下,由点差法可得出直线
的斜率不存在两种情况讨论,在第一种情况下,由点差法可得出直线![]() 的斜率为
的斜率为![]() ,可写出直线
,可写出直线![]() 的方程,即可得出直线
的方程,即可得出直线![]() 所过定点的坐标;在第二种情况下可得出直线
所过定点的坐标;在第二种情况下可得出直线![]() 为
为![]() 轴,即可得出直线
轴,即可得出直线![]() 过定点
过定点![]() ,由此得出结论.
,由此得出结论.
(1)抛物线![]() 的焦点为
的焦点为![]() ,准线为
,准线为![]() .
.
由于抛物线![]() 的准线
的准线![]() 截椭圆
截椭圆![]() 所得弦长为
所得弦长为![]() ,
,
则点![]() 在椭圆
在椭圆![]() 上,则有
上,则有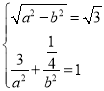 ,解得
,解得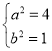 ,
,
因此,椭圆![]() 的标准方程为
的标准方程为![]() ;
;
(2)法一:显然点![]() 在椭圆
在椭圆![]() 内部,故
内部,故![]() ,且直线
,且直线![]() 的斜率不为
的斜率不为![]() .
.
当直线![]() 的斜率存在且不为
的斜率存在且不为![]() 时,易知
时,易知![]() ,设直线
,设直线![]() 的方程为
的方程为![]() ,
,
代入椭圆方程并化简得:![]() .
.
设![]() ,
,![]() ,则
,则![]() ,解得
,解得![]() .
.
因为直线![]() 是线段
是线段![]() 的垂直平分线,
的垂直平分线,
故直线![]() 的方程为
的方程为![]() ,即
,即![]() ,即
,即![]() .
.
令![]() ,此时
,此时![]() ,
,![]() ,于是直线
,于是直线![]() 过定点
过定点![]() ;
;
当直线![]() 的斜率不存在时,易知
的斜率不存在时,易知![]() ,此时直线
,此时直线![]() ,故直线
,故直线![]() 过定点
过定点![]() .
.
综上所述,直线![]() 过定点
过定点![]() ;
;
法二:显然点![]() 在椭圆
在椭圆![]() 内部,故
内部,故![]() ,且直线
,且直线![]() 的斜率不为
的斜率不为![]() .
.
当直线![]() 的斜率存在且不为
的斜率存在且不为![]() 时,设
时,设![]() ,
,![]() ,
,
则有![]() ,
,![]() ,
,
两式相减得![]() ,
,
由线段![]() 的中点为
的中点为![]() ,则
,则![]() ,
,![]() ,
,
故直线![]() 的斜率
的斜率![]() ,
,
因为直线![]() 是线段
是线段![]() 的垂直平分线,
的垂直平分线,
故直线![]() 的方程为
的方程为![]() ,即
,即![]() ,即
,即![]() .
.
令![]() ,此时
,此时![]() ,
,![]() ,于是直线
,于是直线![]() 过定点
过定点![]() ;
;
当直线![]() 的斜率不存在时,易知
的斜率不存在时,易知![]() ,此时直线
,此时直线![]() ,故直线
,故直线![]() 过定点
过定点![]()
综上所述,直线![]() 过定点
过定点![]() .
.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:
【题目】为了纪念“一带一路”倡议提出五周年,某城市举办了一场知识竞赛,为了了解市民对“一带一路”知识的掌握情况,从回收的有效答卷中按青年组和老年组各随机抽取了40份答卷,发现成绩都在![]() 内,现将成绩按区间
内,现将成绩按区间![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 进行分组,绘制成如下的频率分布直方图.
进行分组,绘制成如下的频率分布直方图.
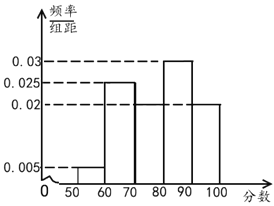
青年组

中老年组
(1)利用直方图估计青年组的中位数和老年组的平均数;
(2)从青年组![]() ,
,![]() 的分数段中,按分层抽样的方法随机抽取5份答卷,再从中选出3份答卷对应的市民参加政府组织的座谈会,求选出的3位市民中有2位来自
的分数段中,按分层抽样的方法随机抽取5份答卷,再从中选出3份答卷对应的市民参加政府组织的座谈会,求选出的3位市民中有2位来自![]() 分数段的概率.
分数段的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,已知菱形![]() 的对角线
的对角线![]() 交于点
交于点![]() ,点
,点![]() 为线段
为线段![]() 的中点,
的中点,![]() ,
,![]() ,将三角形
,将三角形![]() 沿线段
沿线段![]() 折起到
折起到![]() 的位置,
的位置,![]() ,如图2所示.
,如图2所示.

(Ⅰ)证明:平面![]()
![]() 平面
平面![]() ;
;
(Ⅱ)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现将甲、乙两个学生在高二的6次数学测试的成绩(百分制)制成如图所示的茎叶图,进入高三后,由于改进了学习方法,甲、乙这两个学生的考试成绩预计同时有了大的提升:若甲(乙)的高二任意一次考试成绩为![]() ,则甲(乙)的高三对应的考试成绩预计为
,则甲(乙)的高三对应的考试成绩预计为![]() .
.

(1)试预测:高三6次测试后,甲、乙两个学生的平均成绩分别为多少?谁的成绩更稳定?
(2)若已知甲、乙两个学生的高二6次考试成绩分别由低到高进步的,定义![]() 为高三的任意一次考试后甲、乙两个学生的当次成绩之差的绝对值,求
为高三的任意一次考试后甲、乙两个学生的当次成绩之差的绝对值,求![]() 的平均值.
的平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】身体素质拓展训练中,人从竖直墙壁的顶点A沿光滑杆自由下滑到倾斜的木板上(人可看作质点),若木板的倾斜角不同,人沿着三条不同路径AB、AC、AD滑到木板上的时间分别为t1、t2、t3,若已知AB、AC、AD与板的夹角分别为70o、90o和105o,则( )

A. t1>t2>t3 B. t1<t2<t3 C. t1=t2=t3 D. 不能确定t1、t2、t3之间的关系
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年“非洲猪瘟”过后,全国生猪价格逐步上涨,某大型养猪企业,欲将达到养殖周期的生猪全部出售,根据去年的销售记录,得到销售生猪的重量的频率分布直方图(如图所示).
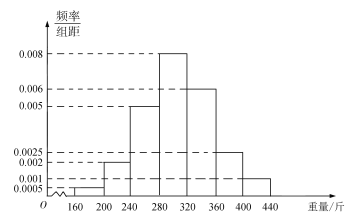
(1)根据去年生猪重量的频率分布直方图,估计今年生猪出栏(达到养殖周期)时,生猪重量达不到270斤的概率(以频率代替概率);
(2)若假设该企业今年达到养殖周期的生猪出栏量为5000头,生猪市场价格是8元/斤,试估计该企业本养殖周期的销售收入是多少万元;
(3)若从本养殖周期的生猪中,任意选两头生猪,其重量达到270斤及以上的生猪数为随机变量![]() ,试求随机变量
,试求随机变量![]() 的分布列及方差.
的分布列及方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,N为CD的中点,M是AC上一点.
中,N为CD的中点,M是AC上一点.
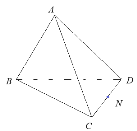
(1)若M为AC的中点,求证:AD//平面BMN;
(2)若![]() ,平面
,平面![]() 平面BCD,
平面BCD,![]() ,求直线AC与平面BMN所成的角的余弦值。
,求直线AC与平面BMN所成的角的余弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求![]() 、
、![]() ;
;
(2)设曲线![]() 与
与![]() 轴负半轴的交点为点
轴负半轴的交点为点![]() ,曲线在点
,曲线在点![]() 处的切线方程为
处的切线方程为![]() ,求证:对于任意的实数
,求证:对于任意的实数![]() ,都有
,都有![]() ;
;
(3)若关于![]() 的方程
的方程![]() 有两个实数根
有两个实数根![]() ,
,![]() ,且
,且![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com