
| A. | (2,+∞) | B. | [2,+∞) | C. | (-∞,2) | D. | (-∞,2] |
分析 首先对y=ax-lnx求导:y'=a-$\frac{1}{x}$;函数y在$(\frac{1}{2},+∞)$内单调递增,即y'在$(\frac{1}{2},+∞)$上恒有y'≥0.即:a≥$\frac{1}{x}$在$(\frac{1}{2},+∞)$上恒成立.
解答 解:首先对y=ax-lnx求导:y'=a-$\frac{1}{x}$,且知y函数的定义域为(0,+∞);
函数y在$(\frac{1}{2},+∞)$内单调递增,即y'在$(\frac{1}{2},+∞)$上恒有y'≥0.
即:a≥$\frac{1}{x}$在$(\frac{1}{2},+∞)$上恒成立.
因为f(x)=$\frac{1}{x}$在$(\frac{1}{2},+∞)$上的最大值为f($\frac{1}{2}$)=2;
所以a的取值范围为a≥2.
故选:B
点评 本题主要考查了利用导数研究函数的单调与恒成立问题,以及转化思想的应用,属中等题.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥S-ABCD中,底面ABCD为平行四边形,AB=3,AC=4,AD=5,SA⊥平面ABCD.
如图,四棱锥S-ABCD中,底面ABCD为平行四边形,AB=3,AC=4,AD=5,SA⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
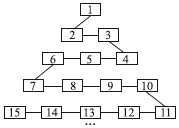 如图是网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行,依此类推,則第20行从左至右的第4个数字应是194.
如图是网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行,依此类推,則第20行从左至右的第4个数字应是194.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com