若tanα=$\frac{1}{2}$.tanβ=$\frac{1}{3}$.则tan=$\frac{1}{7}$．题目和参考答案——青夏教育精英家教网—

17．若tanα=$\frac{1}{2}$，tanβ=$\frac{1}{3}$，则tan（α-β）=$\frac{1}{7}$．

分析根据题意，由正切的差角公式tan（α-β）=$\frac{tanα-tanβ}{1+tanαtanβ}$，将tanα与tanβ的值代入计算可得答案．

解答解：根据题意，tanα=$\frac{1}{2}$，tanβ=$\frac{1}{3}$，
则tan（α-β）=$\frac{tanα-tanβ}{1+tanαtanβ}$=$\frac{\frac{1}{2}-\frac{1}{3}}{1+\frac{1}{2}×\frac{1}{3}}$=$\frac{1}{7}$；
故答案为：$\frac{1}{7}$．

点评本题考查正切的差角公式，解题的关键是熟悉并灵活运用正切的差角公式．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：选择题

7．已知i为虚数单位，若（1+i） z=2i，则复数z=（　　）

A．

1-i

B．

1+i

C．

2-2i

D．

2+2i

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

8．已知命题p：?x∈R，sinx≥-1，则￢p（　　）

A．

?x₀∈R，sinx₀≤-1

B．

?x₀∈R，sinx₀＜-1

C．

?x∈R，sinx≤-1

D．

?x∈R，sinx＜-1

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

5．己知向量$\overrightarrow{s}$=（$\sqrt{3}$sin2x-1，cosx），$\overrightarrow{t}$=（$\frac{1}{2}$，cosx），设f（x）=$\overrightarrow{s}$$•\overrightarrow{t}$+1．
（1）求函数f（x）的最小正周期及在区间[0，$\frac{π}{2}$]上的最大值；
（2）已知在△ABC中，内角A，B，C的对边分别为a，b，c，其中A，B为锐角，f（A+$\frac{π}{6}$）=$\frac{8}{5}$，f（$\frac{B}{2}$$-\frac{π}{12}$）-1=$\frac{\sqrt{10}}{10}$，又a+b=$\sqrt{2}$+1，求a，b，c的值．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

12．

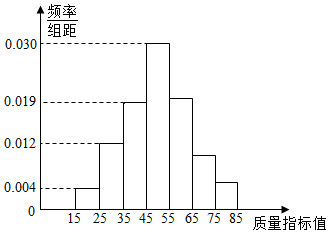从某企业生产的某种产品中抽取100件，测量这些产品的质量指标值，由测量结果得到如图所示的频率分布直方图，质量指标值落在区间[55，65），[65，75），[75，85]内的频率之比为4：2：1．
（I）求这些产品质量指标值落在区间[75，85]内的频率；
（Ⅱ）若将频率视为概率，从该企业生产的这种产品中随机抽取3件，记这3件产品中质量指标值位于区间[45，75）内的产品件数为X，求X的分布列与数学期望．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

2．证明．对于任意两个向量$\overrightarrow{a}$，$\overrightarrow{b}$都有||$\overrightarrow{a}$|-|$\overrightarrow{b}$||≤|$\overrightarrow{a}$-$\overrightarrow{b}$|≤|$\overrightarrow{a}$|+|$\overrightarrow{b}$|．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

9．已知O为坐标原点，B、D分别是单位圆与x轴正半轴、y正半轴的交点，点P为单位圆劣弧$\widehat{BD}$上一点，若$\overrightarrow{OB}$+$\overrightarrow{OD}$=x$\overrightarrow{DB}$+y$\overrightarrow{OP}$，∠BOP=$\frac{π}{3}$，则x+y=（　　）

A．

B．

$\sqrt{3}$

C．

D．

4-3$\sqrt{3}$

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

6．

若函数y=Asin（ωx+φ）的图象如图所示，求它的解析式、频率和振幅．