
分析 (I)利用“以4为界的类斜率函数”的定义,判断给出的区间内|$\frac{f({x}_{1})-f({x}_{2})}{\frac{1}{{x}_{1}}-\frac{1}{{x}_{2}}}$|≤4是否成立即可.
(II)根据f(x)的单调性得出去绝对值号化为:x2+alnx2+$\frac{4}{{x}_{2}}$≤x1+alnx1+$\frac{4}{{x}_{1}}$.g(x)=x+alnx+$\frac{4}{x}$为减函数,令h′(x)≤0恒成立,分离参数得a≤$\frac{4}{x}$-x,令h(x)=$\frac{4}{x}$-x,可得:函数h(x)在区间(0,1]上为减函数.求出h(x)的最小值即可得出a的范围.
解答 解:(I)对任意x1,x2∈(0,1],且x1≠x2,都有|$\frac{f({x}_{1})-f({x}_{2})}{\frac{1}{{x}_{1}}-\frac{1}{{x}_{2}}}$|=$|\frac{\frac{4}{{x}_{1}}-\frac{4}{{x}_{2}}}{{x}_{1}-{x}_{2}}|$=$\frac{4}{{x}_{1}{x}_{2}}$<4,
∴y=$\frac{4}{x}$是“以4为界的类斜率函数”.
(II)f′(x)=1-$\frac{a}{x}$,
∵1≥x>0,a<0,
∴f′(x)>0,
∴f(x)在区间(0,1]上为增函数.
设0<x1<x2≤1,
∵函数f(x)是为“以4为界的类斜率函数”,
∴a<0时,|$\frac{f({x}_{1})-f({x}_{2})}{\frac{1}{{x}_{1}}-\frac{1}{{x}_{2}}}$|=$|\frac{{x}_{1}-1-aln{x}_{1}-({x}_{2}-1-aln{x}_{2})}{\frac{1}{{x}_{1}}-\frac{1}{{x}_{2}}}|$=$\frac{{x}_{2}-{x}_{1}-a(ln{x}_{1}-ln{x}_{2})}{\frac{1}{{x}_{1}}-\frac{1}{{x}_{2}}}$≤4,
化为:x2+alnx2+$\frac{4}{{x}_{2}}$≤x1+alnx1+$\frac{4}{{x}_{1}}$.
令g(x)=x+alnx+$\frac{4}{x}$,则g(x)在区间(0,1]上为减函数.
∴g′(x)=1+$\frac{a}{x}$-$\frac{4}{{x}^{2}}$≤0在区间(0,1]上恒成立,
∴a≤$\frac{4}{x}$-x,
令h(x)=$\frac{4}{x}$-x,可得:函数h(x)在区间(0,1]上为减函数.
∴x=1时,h(x)取得最小值h(1)=3.
∴a≤3.
点评 本题考查了利用导数研究函数的单调性极值与最值、构造函数方法、不等式的性质、新定义,考查了推理能力与计算能力,属于难题.


 互动英语系列答案
互动英语系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
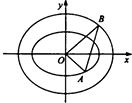 如图,在平面直角坐标系xOy中,A和B分别是椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)和C2:$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{{n}^{2}}$=1(m>n>0)上的动点,已知C1的焦距为2,且$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,又当动点A在x轴上的射影为C1的焦点时,点A恰在双曲线2y2-x2=1的渐近线上.
如图,在平面直角坐标系xOy中,A和B分别是椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)和C2:$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{{n}^{2}}$=1(m>n>0)上的动点,已知C1的焦距为2,且$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,又当动点A在x轴上的射影为C1的焦点时,点A恰在双曲线2y2-x2=1的渐近线上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com