Question

3．小龙与小虎约好国庆节去天柱山游玩，决定十月一日早晨7：45到8：15在高河新车站会面，并约定先到者等候另一人15分钟，若未等到，可直接乘车前往天柱山，求小龙与小虎一同前往天柱山的概率是多少？

Answer 1

分析 由题意知本题是一个几何概型，试验发生包含的所有事件对应的集合是Ω={（x，y）|$7\frac{3}{4}≤x≤8\frac{1}{4}$，$7\frac{3}{4}≤y≤8\frac{1}{4}$}做出集合对应的面积是边长为$\frac{1}{2}$的正方形的面积，写出满足条件的事件对应的集合和面积，根据面积之比得到概率．

解答 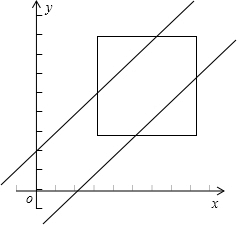解：设小龙和小虎到达高河新车站的时间分别为x、y，则有：$7\frac{3}{4}≤x≤8\frac{1}{4}$，$7\frac{3}{4}≤y≤8\frac{1}{4}$，
当且仅当$|y-x|≤\frac{1}{4}$时，小龙与小虎能一同前往天柱山，
记“小龙与小虎一同前往天柱山”为事件A
则全体事件构成的区域Ω是边长为$\frac{1}{2}$的正方形，因此：${S_Ω}=\frac{1}{4}$
事件A构成的区域为正方形内夹在两平行直线$|y-x|=\frac{1}{4}$之间的部分，
因此：${S_A}=\frac{1}{4}-\frac{1}{16}=\frac{3}{16}$
依据几何概率的计算公式得：$P（A）=\frac{S_A}{S_Ω}=\frac{3}{4}$
所以：小龙与小虎一同前往天柱山的概率是$\frac{3}{4}$．

点评 本题考查几何概型，难点是把时间分别用x，y坐标来表示，从而把时间长度问题转化为平面图形的面积问题，转化成面积型的几何概型问题，是中档题．