
分析 根据向量垂直的条件和向量的数量积公式即可求出.
解答 解:∵向量$λ\overrightarrow a+\overrightarrow b$与$\overrightarrow a+2\overrightarrow b$垂直,向量$\overrightarrow a$,$\overrightarrow b$为单位向量且夹角为$\frac{π}{3}$,
∴($λ\overrightarrow a+\overrightarrow b$)($\overrightarrow a+2\overrightarrow b$)=0,
∴λ${\overrightarrow{a}}^{2}$+(2λ+1)$\overrightarrow{a}$•$\overrightarrow{b}$+2${\overrightarrow{b}}^{2}$=λ+(2λ+1)×$\frac{1}{2}$+2=0,
∴λ=-$\frac{5}{4}$
故答案为:-$\frac{5}{4}$
点评 本题考查了向量垂直的条件和向量的数量积公式,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
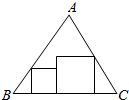 从等边三角形纸片ABC上,剪下如图所示的两个正方形,其中BC=3+$\sqrt{3}$,则这两个正方形的面积之和的最小值为$\frac{9}{2}$.
从等边三角形纸片ABC上,剪下如图所示的两个正方形,其中BC=3+$\sqrt{3}$,则这两个正方形的面积之和的最小值为$\frac{9}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某科技研究所对一批新研发的产品长度进行检测(单位:mm),如图是检测结果的频率分布直方图,据此估计这批产品的中位数为( )
某科技研究所对一批新研发的产品长度进行检测(单位:mm),如图是检测结果的频率分布直方图,据此估计这批产品的中位数为( )| A. | 20 | B. | 22.5 | C. | 22.75 | D. | 25 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
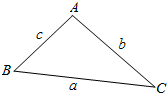 (1)如图所示.在△ABC中,射影定理可表示为a=b•cosC+c•cosB.其中a,b,c分别为角A,B,C的对边,类比上述定理.写出对空间四面体性质的猜想.
(1)如图所示.在△ABC中,射影定理可表示为a=b•cosC+c•cosB.其中a,b,c分别为角A,B,C的对边,类比上述定理.写出对空间四面体性质的猜想.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com