
分析 (Ⅰ)根据sin2θ+cos2θ=1,求出C1的普通方程,根据x=ρcosθ,y=ρsinθ,求出C2的普通方程即可;
(Ⅱ)联立方程组,求出AB的中点坐标,从而求出AB的中垂线方程即可.
解答 解 (Ⅰ)∵曲线C1:$\left\{\begin{array}{l}x=\sqrt{2}cosθ\\ y=sinθ\end{array}$(其中θ为参数),
∴C1:$\frac{x^2}{2}$+y2=1
∵曲线${C_2}:ρcos(θ-\frac{π}{4})=\frac{{\sqrt{2}}}{4}$,
∴ρ($\frac{\sqrt{2}}{2}$cosθ+$\frac{\sqrt{2}}{2}$sinθ)=$\frac{\sqrt{2}}{4}$,
由x=ρcosθ,y=ρsinθ得:
C2:2x+2y-1=0…(5分)
(Ⅱ)设A(x1,y1),B(x2,y2),
联立方程组$(\begin{array}{l}\frac{x^2}{2}+{y^2}=1,\\ y=-x+\frac{1}{2}.\end{array}\right.$,得:3x2-2x-$\frac{3}{2}$=0,
则 x1+x2=$\frac{2}{3}$.∴AB中点坐标为($\frac{1}{3}$,$\frac{1}{6}$).
∴AB的中垂线的参数方程为$(\begin{array}{l}x=\frac{1}{3}+\frac{{\sqrt{2}}}{2}t,\\ y=\frac{1}{6}+\frac{{\sqrt{2}}}{2}t.\end{array}\right.$(t为参数) …(12分)
( 方程写成$(\begin{array}{l}x=\frac{1}{3}+t,\\ y=\frac{1}{6}+t.\end{array}\right.$(t为参数) 等均可 )
点评 本题考查了直角坐标方程、极坐标方程以及参数方程的转化及其应用,是一道中档题.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:选择题
| A. | (log2x)′=$\frac{1}{xln2}$ | B. | (x+$\frac{1}{x}$)′=1+$\frac{1}{{x}^{2}}$ | ||
| C. | (cosx)′=sinx | D. | ($\frac{{e}^{x}}{x}$)′=$\frac{x{e}^{x}+{e}^{x}}{{x}^{2}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 年龄为37岁的人体内脂肪含量都为20.90% | |
| B. | 年龄为37岁的人体内脂肪含量为21.01% | |
| C. | 年龄为37岁的人群中的大部分人的体内脂肪含量为20.90% | |
| D. | 年龄为37岁的大部分的人体内脂肪含量为31.50% |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 ,其中A的各位数字中,a1=1,且ak(k=2,3,4,5)为0和1的概率分别是$\frac{1}{4}$和$\frac{3}{4}$.记ξ=a1+a2+a3+a4+a5,当程序运行一次时:
,其中A的各位数字中,a1=1,且ak(k=2,3,4,5)为0和1的概率分别是$\frac{1}{4}$和$\frac{3}{4}$.记ξ=a1+a2+a3+a4+a5,当程序运行一次时:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在正方体ABCD-A'B'C'D'中,E为DD'的中点.
如图,在正方体ABCD-A'B'C'D'中,E为DD'的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数是周期为2π的偶函数 | B. | 函数是周期为π的偶函数 | ||
| C. | 函数是周期为2π的奇函数 | D. | 函数是周期为π的奇函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
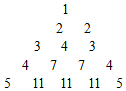 观察如图所示的”三角数阵”
观察如图所示的”三角数阵”查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com