
 已知椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的右焦点F(1,0),离心率为$\frac{{\sqrt{2}}}{2}$,过F作两条互相垂直的弦AB,CD,设AB,CD的中点分别为M,N.
已知椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的右焦点F(1,0),离心率为$\frac{{\sqrt{2}}}{2}$,过F作两条互相垂直的弦AB,CD,设AB,CD的中点分别为M,N.分析 (1)根据题意确定出c与e的值,利用离心率公式求出a的值,进而求出b的值,确定出椭圆方程即可;
(2)由直线AB与CD向量存在,设为k,表示出AB方程,设出A与B坐标,进而表示出M坐标,联立直线AB与椭圆方程,消去y得到关于x的一元二次方程,利用根与系数的关系表示出M,同理表示出N,根据M与N横坐标相同求出k的值,得到此时MN斜率不存在,直线MN恒过定点;若直线MN斜率存在,表示出直线MN斜率,进而表示出直线MN,令y=0,求出x的值,得到直线MN恒过定点,综上,得到直线MN恒过定点,求出定点坐标即可;
(3)根据P坐标,得到OP的长,由OF-OP表示出PF长,三角形MNF面积等于三角形PMF面积加上三角形PNF面积,利用基本不等式求出面积的最大值即可.
解答 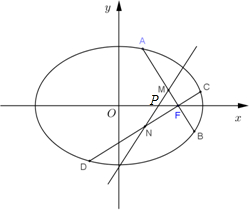 解:(1)由题意:c=1,$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,
解:(1)由题意:c=1,$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,
∴a=$\sqrt{2}$,b=c=1,
则椭圆的方程为$\frac{{x}^{2}}{2}$+y2=1;
(2)∵AB,CD斜率均存在,
∴设直线AB方程为:y=k(x-1),
再设A(x1,y1),B(x2,y2),则有M($\frac{{x}_{1}+{x}_{2}}{2}$,k($\frac{{x}_{1}+{x}_{2}}{2}$-1)),
联立得:$\left\{{\begin{array}{l}{y=k(x-1)}\\{{x^2}+2{y^2}-2=0}\end{array}}\right.$,
消去y得:(1+2k2)x2-4k2x+2k2-2=0,
∴$\left\{{\begin{array}{l}{{x_1}+{x_2}=\frac{{4{k^2}}}{{1+2{k^2}}}}\\{{x_1}{x_2}=\frac{{2{k^2}-2}}{{1+2{k^2}}}}\end{array}}\right.$,即M($\frac{2{k}^{2}}{1+2{k}^{2}}$,$\frac{-k}{1+2{k}^{2}}$),
将上式中的k换成-$\frac{1}{k}$,同理可得:N($\frac{2}{2+{k}^{2}}$,$\frac{k}{2+{k}^{2}}$),
若$\frac{2{k}^{2}}{1+2{k}^{2}}$=$\frac{2}{2+{k}^{2}}$,解得:k=±1,直线MN斜率不存在,
此时直线MN过点($\frac{2}{3}$,0);
下证动直线MN过定点P($\frac{2}{3}$,0),
若直线MN斜率存在,则kMN=$\frac{\frac{-k}{1+2{k}^{2}}-\frac{k}{2+{k}^{2}}}{\frac{2{k}^{2}}{1+2{k}^{2}}-\frac{2}{2+{k}^{2}}}$=$\frac{-k(3{k}^{2}+3)}{2{k}^{4}-2}$=$\frac{3}{2}$×$\frac{-k}{{k}^{2}-1}$,
直线MN为y-$\frac{k}{2+{k}^{2}}$=$\frac{3}{2}$×$\frac{-k}{{k}^{2}-1}$(x-$\frac{2}{2+{k}^{2}}$),
令y=0,得x=$\frac{2}{2+{k}^{2}}$+$\frac{2}{3}$×$\frac{{k}^{2}-1}{2+{k}^{2}}$=$\frac{2}{3}$×$\frac{3+{k}^{2}-1}{2+{k}^{2}}$=$\frac{2}{3}$,
综上,直线MN过定点($\frac{2}{3}$,0);
(3)由第(2)问可知直线MN过定点P($\frac{2}{3}$,0),
故S△FMN=S△FPM+S△FPN=$\frac{1}{2}$×$\frac{1}{3}$|$\frac{k}{2+{k}^{2}}$|+$\frac{1}{2}$×$\frac{1}{3}$|$\frac{-k}{1+2{k}^{2}}$=$\frac{1}{2}$×$\frac{(|k|+\frac{1}{|k|})}{2{k}^{2}+\frac{2}{{k}^{2}}+5}$,
令t=|k|+$\frac{1}{|k|}$∈[2,+∞),S△FMN=f(t)=$\frac{1}{2}$×$\frac{t}{2({t}^{2}-2)+5}$=$\frac{1}{2}$×$\frac{t}{2{t}^{2}+1}$,
∴f(t)在t∈[2,+∞)单调递减,
当t=2时,f(t)取得最大值,即S△FMN最大值$\frac{1}{9}$,此时k=±1.
点评 此题考查了椭圆的简单性质,根与系数的关系,中点坐标公式,以及直线两点式方程,熟练掌握椭圆的简单性质是解本题的关键.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{5}{8}$ | C. | $\frac{1}{2}$ | D. | $\frac{7}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
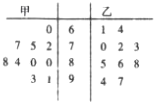 某学校甲、乙两个班各派10名同学参加英语口语比赛,并记录他们的成绩,得到如图所示的茎叶图.现拟定在各班中分数超过本班平均分的同学为“口语王”.
某学校甲、乙两个班各派10名同学参加英语口语比赛,并记录他们的成绩,得到如图所示的茎叶图.现拟定在各班中分数超过本班平均分的同学为“口语王”.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\sqrt{2}$,-$\sqrt{2}$) | B. | (1,-1) | C. | (1,-i) | D. | (2,-2i) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 重心 | B. | 垂心 | C. | 外心 | D. | 内心 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{4}-{y^2}$=1 | B. | $\frac{x^2}{3}-\frac{y^2}{12}$=1 | C. | $\frac{x^2}{12}-\frac{y^2}{3}$=1 | D. | ${x^2}-\frac{y^2}{4}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -15 | B. | 15 | C. | -16 | D. | 16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com