
分析 (1)把b=$\frac{1}{6}$代入函数解析式,求出导函数,由f′(x)=$3a{x}^{2}+\frac{1}{6}$>0,可知f(x)在[-3,3]上为增函数,求出函数的最小值,由最小值大于0求得a的取值范围;
(2)①求出函数的导函数,解得导函数的零点,然后根据$\sqrt{-\frac{b}{3a}}$与3的关系分类求得函数的单调区间;
②当b<-1时,由①可知,当0<a≤$-\frac{b}{27}$时,f(x)在[-3,3]上单调递减,求得函数的最小值小于0,这与?x∈D,f(x)≥0恒成立矛盾,故此时实数a不存在;
当a>-$\frac{b}{27}$时,由①可得f(x)min={f(-3),f($\sqrt{-\frac{b}{3a}}$)},若f(-3)=-27a-3b+1<0,这与?x∈D,f(x)≥0恒成立矛盾,故此时实数a不存在;若f(-3)=-27a-3b+1>0,证明f($\sqrt{-\frac{b}{3a}}$)<0,这与?x∈D,f(x)≥0恒成立矛盾,故此时实数a不存在.
解答 (1)解:当b=$\frac{1}{6}$时,f(x)=$a{x}^{3}+\frac{1}{6}x+1$,f′(x)=$3a{x}^{2}+\frac{1}{6}$>0,
∴f(x)在[-3,3]上为增函数,则$f(x)_{min}=f(-3)=-27a-\frac{1}{2}+1$=$\frac{1}{2}-27a$.
由$\frac{1}{2}-27a≥0$,解得a$≤\frac{1}{54}$.
∴A={a|?x∈D,f(x)≥0}=(0,$\frac{1}{54}$];
(2)①解:f(x)=ax3+bx+1,f′(x)=3ax2+b,
∵a>0,b<0,
∴由f′(x)=3ax2+b=0,得${x}^{2}=-\frac{b}{3a}$>0,则x=$±\sqrt{-\frac{b}{3a}}$.
若27a+b≤0,则$\sqrt{-\frac{b}{3a}}≥3$,则f′(x)≤0在[-3,3]上恒成立,f(x)在[-3,3]上为减函数;
若27a+b>0,则当x∈[-3,$-\sqrt{-\frac{b}{3a}}$)∪($\sqrt{-\frac{b}{3a}}$,3]时,f′(x)>0,
当x∈($-\sqrt{-\frac{b}{3a}},\sqrt{-\frac{b}{3a}}$)时,f′(x)<0.
∴函数的增区间为[-3,$-\sqrt{-\frac{b}{3a}}$),($\sqrt{-\frac{b}{3a}}$,3],减区间为($-\sqrt{-\frac{b}{3a}},\sqrt{-\frac{b}{3a}}$);
②证明:当b<-1时,由①可知,当0<a≤$-\frac{b}{27}$时,f(x)在[-3,3]上单调递减,
∴f(x)min=f(3)=27a+3b+1≤-b+3b+1=2b+1<-1<0,
这与?x∈D,f(x)≥0恒成立矛盾,故此时实数a不存在;
当a>-$\frac{b}{27}$时,f(x)在[-3,$-\sqrt{-\frac{b}{3a}}$),($\sqrt{-\frac{b}{3a}}$,3]上递增,在($-\sqrt{-\frac{b}{3a}},\sqrt{-\frac{b}{3a}}$)上递减,
∴f(x)min={f(-3),f($\sqrt{-\frac{b}{3a}}$)},
若f(-3)=-27a-3b+1<0,这与?x∈D,f(x)≥0恒成立矛盾,故此时实数a不存在;
若f(-3)=-27a-3b+1>0,令${x}_{1}=\sqrt{-\frac{b}{3a}}$,此时f(x1)=$a{{x}_{1}}^{3}+b{x}_{1}+1$.
又f′(x1)=$3a{{x}_{1}}^{2}+b=0$,则$a{{x}_{1}}^{2}=-\frac{b}{3}$.
f(x1)=$a{{x}_{1}}^{3}+b{x}_{1}+1={x}_{1}(-\frac{b}{3})+b{x}_{1}+1$=$\frac{2b}{3}\sqrt{-\frac{b}{3a}}+1=-\sqrt{-\frac{4{b}^{3}}{27a}}+1$.
下面证明$-\sqrt{-\frac{4{b}^{3}}{27a}}+1<0$,也即证-4b3>27a,
∵a>-$\frac{b}{27}$,且-27a-3b+1>0,即27a<-3b+1.
再证-4b3>-3b+1,
令g(b)=4b3-3b+1,则g′(b)=12b2-3>0(b<-1),
∴g(b)在(-∞,-1]上单调递增,则g(b)<g(-1)=0.
即f(x1)<0,这与?x∈D,f(x)≥0恒成立矛盾,故此时实数a不存在.
综上所述,A=∅.?
点评 本题考查利用导数研究函数的单调性,考查利用导数求函数的最值,考查数学转化思想方法、逻辑思维能力、灵活变形能力及推理运算能力,难度较大.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | $\frac{4}{5}i$ | C. | $\frac{6}{5}$ | D. | $\frac{6}{5}i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+2+22+…+2k-2+2k-1=2k+1-1 | B. | 1+2+22+…+2k+2k+1=2k-1+2k+1 | ||
| C. | 1+2+22+…+2k-1+2k+1=2k+1-1 | D. | 1+2+22+…+2k-1+2k=2k+1-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
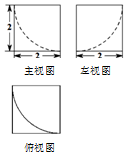
| A. | $8-\frac{4}{3}π$ | B. | $8-\frac{8}{3}π$ | C. | 24-π | D. | 24+π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | 1或$\frac{1}{2}$ | D. | 无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com