练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

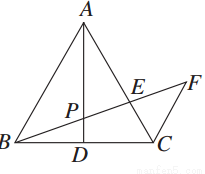
    如图，△ABC中，AB＝AC，AD是中线，P为AD上一点，CF∥AB，BP延长线交AC、CF于E、F，求证：PB2＝PE·PF．

     

     

    见解析

    【解析】证明：连接PC，易证PC＝PB，∠ABP＝∠ACP．

    ∵CF∥AB，∴∠F＝∠ABP，从而∠F＝∠ACP．

    又∠EPC为△CPE与△FPC的公共角，

    从而△CPE∽△FPC，∴＝，

    ∴PC2＝PE·PF．

    又PC＝PB，∴PB2＝PE·PF．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2016届云南省高一下学期期末考试数学试卷（解析版） 题型：选择题

    已知向量，若与垂直，则( ).

    A． B． C．1 D．4

     

    查看答案和解析>>

    科目：高中数学 来源：2016届上海市高一下学期期末考试数学试卷（解析版） 题型：填空题

    设为等差数列的前项和，若，公差，，则 ．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：选4-1-2直线与圆的位置关系（解析版） 题型：填空题

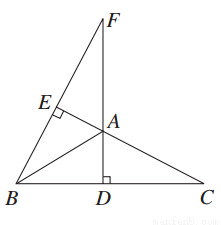
    如图，已知圆中两条弦AB与CD相交于点F，E是AB延长线上一点，且DF＝CF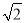＝，AF∶FB∶BE＝4∶2∶1，若CE与圆相切，则线段CE的长为________．

     

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：选4-1-1相似三角形判定及性质（解析版） 题型：填空题

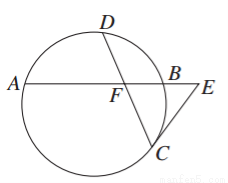
    如图，△ABC中，BC＝4，∠BAC＝120°，AD⊥BC，过B作CA的垂线，交CA的延长线于E，交DA的延长线于F，则AF＝________．

     

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：选4-1-1相似三角形判定及性质（解析版） 题型：选择题

    如图，在平行四边形ABCD中，E为CD上一点，DE∶EC＝2∶3，连接AE，BE，BD，且AE，BD交于点F，则S△DEF∶S△EBF∶S△ABF＝(　　)

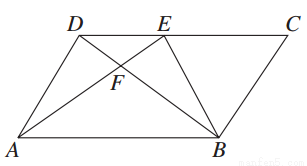
    A．4∶10∶25 B．4∶9∶25

    C．2∶3∶5 D．2∶5∶25

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：9-4算法初步（解析版） 题型：选择题

    已知某流程图如图所示，现分别输入选项中所述的四个函数，则可以输出的函数是(　　)

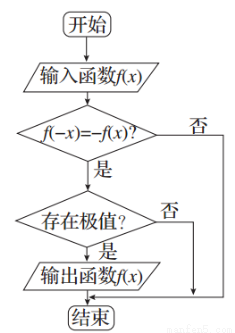
    A．f(x)＝2x4＋3x2 B．f(x)＝x3

    C．f(x)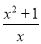＝ D．f(x)＝x2＋1

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：9-2用样本估计总体（解析版） 题型：填空题

    某班有48名学生，在一次考试中统计出平均分为70，方差为75，后来发现有2名同学的分数登记错了，甲实际得80分却记成了50分，乙实际得70分却记成了100分，更正后平均分为________，方差为________．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：8-8曲线与方程（解析版） 题型：填空题

    若过点P(1,1)且互相垂直的两条直线l1，l2分别与x轴，y轴交于A，B两点，则AB中点M的轨迹方程为________．

     

    查看答案和解析>>

    同步练习册答案