
分析 若“p∨q”为真命题,“p∧q”为假命题,则p,q一真一假,进而可得m取值范围.
解答 解:命题p为真?△=(2m-3)2-4>0?$m<\frac{1}{2}或m>\frac{5}{2}$…(3分)
若命题q为真?m>2…(5分)
∵“p且q”是假命题,“p或q”是真命题
∴p,q一真一假 …(7分)
若p真q假,则$\left\{\begin{array}{l}m<\frac{1}{2}或m>\frac{5}{2}\\ m≤2\end{array}\right.$∴$m<\frac{1}{2}$…(9分)
若q真p假,则$\left\{\begin{array}{l}\frac{1}{2}≤m≤\frac{5}{2}\\ m>2\end{array}\right.$∴$2<m≤\frac{5}{2}$…(11分)
综上,$m<\frac{1}{2}$或$2<m≤\frac{5}{2}$…(12分)
点评 本题以命题的真假判断与应用为载体,考查了复合命题,二次函数的图象和性质,椭圆的标准方程,难度中档.


科目:高中数学 来源: 题型:选择题
| A. | 1,π | B. | 1,4π | C. | $\frac{3}{2},π$ | D. | $\frac{3}{2},4π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | $2\sqrt{3}$ | C. | $4\sqrt{3}$ | D. | $2\sqrt{15}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-∞,\frac{e}{3})$ | B. | $(\frac{e}{3},{e^2})$ | C. | $(\frac{e}{3},\frac{e^2}{6})$ | D. | $(\frac{e}{3},+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
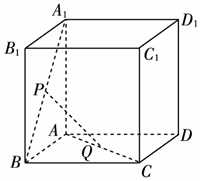 如图所示,已知P、Q是单位正方体ABCD-A1B1C1D1的面A1B1BA和面ABCD对角线上的点,且A1P=AQ,证明:PQ∥平面BCC1B1.
如图所示,已知P、Q是单位正方体ABCD-A1B1C1D1的面A1B1BA和面ABCD对角线上的点,且A1P=AQ,证明:PQ∥平面BCC1B1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 5 | C. | 15 | D. | 25 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com