Question

6．设f（x）满足：①任意x∈R，有f（x）+f（2-x）=0；②当x≥1时，f（x）=|x-a|-1，（a＞0），若x∈R，恒有f（x）＞f（x-m），则m的取值范围是（　　）

• A． （0，+∞）
• B． （4，+∞）
• C． （3，+∞）
• D． （5，+∞）

Answer 1

分析 根据函数的对称性求出a的值，作出函数f（x）的图象，利用数形结合以及图象关系进行平移计算即可．

解答 解：∵任意x∈R，有f（x）+f（2-x）=0，
∴f（2-x）=-f（x），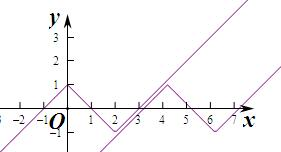
则函数关于（1，0）点对称，
当x=1时，f（1）+f（2-1）=0，即2f（1）=0，
则f（1）=0，
∵当x≥1时，f（x）=|x-a|-1，
∴f（1）=|1-a|-1=0，
则|a-1|=1，则a-1=1或a-1=-1，
则a=2或a=0，
∵a＞0，
∴a=2，
即当x≥1时，f（x）=|x-2|-1
当x≤1时，-x≥-1，2-x≥1，
即f（x）=-f（2-x）=-（|2-x-2|-1）=1-|x|，x≤1，
作出函数f（x）的图象如图：
若f（x）＞f（x-m），则由图象知，将函数f（x）向右平移m个单位即可，
由图象知，m＞4，
故选：B

点评 本题主要考查函数图象的应用，根据函数的对称性求出函数的解析式，以及利用图象平移是解决本题的关键．综合性较强，有一定的难度．