
分析 (1)当n=1时,f(1)=1=g(1);当n=2时,f(2)=$\frac{9}{8}$,g(2)=$\frac{11}{8}$,f(2)<g(2);同理可得:当n=3时,f(3)<g(3).
(2)由(1)猜想:f(n)≤g(n),利用数学归纳法证明即可.
解答 解:(1)当n=1时,f(1)=1=g(1);
当n=2时,f(2)=$\frac{9}{8}$,g(2)=$\frac{11}{8}$,∴f(2)<g(2);
当n=3时,f(3)=$\frac{251}{216}$,g(3)=$\frac{312}{216}$,∴f(3)<g(3).
(2)由(1)猜想:f(n)≤g(n),下面利用数学归纳法证明:①当n=1,2,3时,不等式成立.
②假设当n=k(k∈N*)(k≥3)时,不等式成立,即1+$\frac{1}{{2}^{2}}$+$\frac{1}{{3}^{2}}$+…+$\frac{1}{{k}^{2}}$<$\frac{1}{2}$(3-$\frac{1}{{k}^{2}}$).
则当n=k+1时,则f(k+1)=f(k)+$\frac{1}{(k+1)^{2}}$$<\frac{1}{2}(3-\frac{1}{{k}^{2}})$+$\frac{1}{(k+1)^{2}}$,
∵$\frac{1}{2(k+1)^{2}}-\frac{1}{2{k}^{2}}$+$\frac{1}{(k+1)^{2}}$=$\frac{-3k-1}{2(k+1)^{2}{k}^{2}}$<0,∴$-\frac{1}{2{k}^{2}}+\frac{1}{(k+1)^{2}}$$<-\frac{1}{2(k+1)^{2}}$,
∴f(k+1)<$\frac{3}{2}-\frac{1}{2(k+1)^{2}}$=g(k+1),即当n=k+1时,不等式成立.由①②可知:对?n∈N*,都有f(n)≤g(n).
点评 本题考查了数学归纳法的应用、观察分析猜想归纳能力,考查了计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
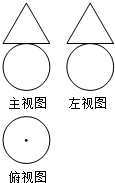 某几何体的三视图如图所示,其中三角形的三边长与圆的直径均为2,则该几何体的表面积为( )
某几何体的三视图如图所示,其中三角形的三边长与圆的直径均为2,则该几何体的表面积为( )| A. | $\frac{4+\sqrt{3}}{3}$π | B. | 5π | C. | 6π | D. | 7π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com