练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．（1-x）3（1+x）10展开式中x5的系数为-63．

    分析 根据（1-x）3（1+x）10展开式中各项的特征，得出展开式中x5的系数是由两个二项展开式的项组成，由此求出答案．

    解答 解：∵（1-x）3（1+x）10=[${C}_{3}^{0}$+${C}_{3}^{1}$•（-x）+${C}_{3}^{2}$•（-x）2+${C}_{3}^{3}$•（-x）3]
    •（${C}_{10}^{0}$+${C}_{10}^{1}$•x+${C}_{10}^{2}$•x2+${C}_{10}^{3}$•x3+${C}_{10}^{4}$•x4+${C}_{10}^{5}$•x5+…）
    =（1-3x+3x2-x3）（1+10x+45x2+120x3+210x4+252x5+…）
    =（1×252-3×210+3×120-1×45）x5+…；
    ∴展开式中x5的系数是252-630+360-45=-63．
    故答案为：-63．

    点评 本题考查了二项式展开式的应用问题，也考查了逻辑思维能力与计算能力，是基础题目．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    15．算式40-20=4×5中，在横线中填入两个正整数，使它们的乘积最大．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．安排甲、乙、丙、丁四人参加周一至周六的公益活动，每天只需一人参加，其中甲参加三天活动，乙、丙、丁每人参加一天，那么甲连续三天参加活动的概率为（　　）
    A．$\frac{1}{15}$B．$\frac{1}{5}$C．$\frac{1}{4}$D．$\frac{1}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．已知f（n）=1+$\frac{1}{{2}^{2}}$+$\frac{1}{{3}^{2}}$+…+$\frac{1}{{n}^{2}}$，g（n）=$\frac{1}{2}$（3-$\frac{1}{{n}^{2}}$），n∈N*．
    （1）当n=1，2，3时，试比较f（n）与g（n）的大小关系；
    （2）猜想f（n）与g（n）的大小关系，并用数学归纳法证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

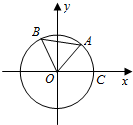    16．如图，点A，B是单位圆上的两点，A，B两点分别在第一、二象限，点C是圆与x轴正半轴的交点，△AOB是正三角形，若点A的坐标为（$\frac{3}{5}$，$\frac{4}{5}$），记∠COA=α．
    （Ⅰ）求$\frac{1+sin2α}{1+cos2α}$的值；
    （Ⅱ）求cos∠COB的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．sin600°=（　　）
    A．$-\frac{{\sqrt{3}}}{2}$B．$-\frac{1}{2}$C．$\frac{1}{2}$D．$\frac{{\sqrt{3}}}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．已知椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}$+y2=1（a＞1），上顶点为A，左顶点为B，设P是椭圆上的任一点，则△PAB的最大值为$\sqrt{2}$+1，若已知M（-$\sqrt{3}$，0），N（$\sqrt{3}$，0），点Q为椭圆上的任意一点，则$\frac{1}{|QN|}+\frac{4}{|QM|}$的最小值为$\frac{9}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．下列类比推理中，结论正确的个数是（　　）
    ①由a（b+c）=ab+ac类比得到loga（x+y）=logax+logay
    ②由a（b+c）=ab+ac类比得到sin（x+y）=sinx+siny
    ③由（ab）n=anbn类比得到（x+y）n=xn+yn
    ④由（a+b）+c=a+（b+c）类比得到（xy）z=x（yz）
    A．0B．1C．2D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知向量$\overrightarrow{a}$=（cos$\frac{3}{2}$x，sin$\frac{3}{2}$x），$\overrightarrow{b}$=（cos$\frac{x}{2}$，sin$\frac{x}{2}$），且x∈[0，$\frac{2π}{3}$]．
    （1）求$\overrightarrow{a}$•$\overrightarrow{b}$及|$\overrightarrow{a}$+$\overrightarrow{b}$|；
    （2）若f（x）=$\overrightarrow{a}$•$\overrightarrow{b}$-2λ|$\overrightarrow{a}$+$\overrightarrow{b}$|的最小值为-$\frac{3}{2}$，求实数λ的值．

    查看答案和解析>>

    同步练习册答案