
分析 由新定义,可得由f(x)=x,g(x)=x,所以f′(x)=1,g′(x)=1,所以y′=(1•lnx+x•$\frac{1}{x}$)xx,令x=1即可得到切线的斜率,再由点斜式方程,可得切线方程.
解答 解:由f(x)=x,g(x)=x,
所以f′(x)=1,g′(x)=1,所以y′=(1•lnx+x•$\frac{1}{x}$)xx,
所以y′|x=1=[(1•lnx+x•$\frac{1}{x}$)xx]x=1=1,
即:函数y=xx(x>0)在(1,1)处的切线的斜率为1,
故切线方程为:y-1=x-1,即y=x,
故答案为:y=x.
点评 本题考查导数的运用:求切线方程,同时考查对数法求导数的方法,考查运算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
 如图,矩形长为6,宽为4,在矩形内随机地撒300颗黄豆,数得落在椭圆内的黄豆数为225颗,以此实验数据为依据可以估计出椭圆的面积约为( )
如图,矩形长为6,宽为4,在矩形内随机地撒300颗黄豆,数得落在椭圆内的黄豆数为225颗,以此实验数据为依据可以估计出椭圆的面积约为( )| A. | 16 | B. | 17 | C. | 18 | D. | 19 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (0,1] | C. | (-∞,0)∪(1,+∞) | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | C${\;}_{7}^{1}$×$\frac{1}{3}$×($\frac{2}{3}$) | B. | C${\;}_{7}^{2}$×($\frac{1}{3}$)2×($\frac{2}{3}$)5 | C. | C${\;}_{7}^{3}$×($\frac{1}{3}$)3×($\frac{2}{3}$) | D. | C${\;}_{7}^{4}$×($\frac{1}{3}$)4×($\frac{2}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
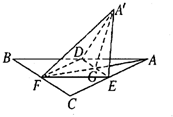 如图,等边三角形ABC的中线AF与中位线DE相交于G,已知△A′ED是△ADE绕DE旋转过程中的一个图形,下列命题中,错误的是( )
如图,等边三角形ABC的中线AF与中位线DE相交于G,已知△A′ED是△ADE绕DE旋转过程中的一个图形,下列命题中,错误的是( )| A. | 异面直线A′E与BD不可能垂直 | |
| B. | 恒有平面A′GF⊥平面BCDE | |
| C. | 三棱锥A′-EFD的体积有最大值 | |
| D. | 动点A′在平面ABC上的射影在线段AF上 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com