
分析 利用递推关系可得:an=-2an-1,再利用等比数列的通项公式即可得出.
解答 解:∵Sn=$\frac{2}{3}$an-$\frac{2}{3}$,
∴当n=1时,${a}_{1}=\frac{2}{3}{a}_{1}$-$\frac{2}{3}$,解得a1=-2.
当n≥2时,an=Sn-Sn-1=$\frac{2}{3}$an-$\frac{2}{3}$-$(\frac{2}{3}{a}_{n-1}-\frac{2}{3})$,化为:an=-2an-1.
∴数列{an}是等比数列,首项与公比都为-2.
∴an=(-2)n.
故答案为:(-2)n.
点评 本题考查了递推关系、等比数列的通项公式,考查了推理能力与计算能力,属于中档题.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:高中数学 来源: 题型:选择题
| A. | 4an=1-3Sn | B. | 4Sn=3an-1 | C. | 4Sn=3an+1 | D. | 4an=3Sn+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
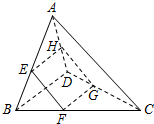 如图,在四面体A-BCD中,AC与BD互相垂直,且长度分别为2和3,平行于这两条棱的平面与边AB、BC、CD、DA分别相交于点E、F、G、H,记四边形EFGH的面积为y,设$\frac{BE}{AB}$=x,则( )
如图,在四面体A-BCD中,AC与BD互相垂直,且长度分别为2和3,平行于这两条棱的平面与边AB、BC、CD、DA分别相交于点E、F、G、H,记四边形EFGH的面积为y,设$\frac{BE}{AB}$=x,则( )| A. | 函数f(x)的值域为(0,1] | B. | 函数y=f(x)满足f(x)=f(2-x) | ||
| C. | 函数y=f(x)的最大值为2 | D. | 函数y=f(x)在(0,$\frac{1}{2}$)上单调递增 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
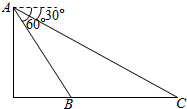 如图,从高为$200\sqrt{3}$米的气球(A)上测量铁桥(BC)的长,如果测得桥头B的俯角是60°,桥头C的俯角是30°,则桥BC长为400米.
如图,从高为$200\sqrt{3}$米的气球(A)上测量铁桥(BC)的长,如果测得桥头B的俯角是60°,桥头C的俯角是30°,则桥BC长为400米.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 射击环数 | 频数 | 频率 |
| 7 | 10 | |
| 8 | 10 | |
| 9 | x | |
| 10 | 30 | y |
| 合计 | 100 | 1 |
| 射击环数 | 频数 | 频率 |
| 7 | 6 | |
| 8 | 10 | |
| 9 | z | 0.4 |
| 10 | ||
| 合计 | 80 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直角三角形 | B. | 等腰三角形 | C. | 等腰直角三角形 | D. | 等边三角形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com