
已知函数
(1)求函数 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;
(2)在 中,A、B、C分别为三边
中,A、B、C分别为三边 所对的角,若
所对的角,若 ,求
,求 的最大值.
的最大值.
(1) ,函数的单调递增区间为
,函数的单调递增区间为 ;(2)因此
;(2)因此 的最大值为
的最大值为 .
.
解析试题分析:(1)将函数 的解析式第一、三项结合,利用二倍角的余弦函数公式化简,第二项利用二倍角的正弦函数公式化简,合并后提取
的解析式第一、三项结合,利用二倍角的余弦函数公式化简,第二项利用二倍角的正弦函数公式化简,合并后提取 ,再利用两角和与差的正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,找出
,再利用两角和与差的正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,找出 的值,代入周期公式
的值,代入周期公式 ,即可求出函数的最小正周期,由正弦函数的递增区间列出关于
,即可求出函数的最小正周期,由正弦函数的递增区间列出关于 的不等式,求出不等式的解集即可得到
的不等式,求出不等式的解集即可得到 的递增区间;(2)由
的递增区间;(2)由 及确定出的
及确定出的 的解析式,变形后利用特殊角的三角函数值求出
的解析式,变形后利用特殊角的三角函数值求出 的度数,可得出
的度数,可得出 的值,再由
的值,再由 的值,利用余弦定理列出关系式,将
的值,利用余弦定理列出关系式,将 与
与 的值代入,利用完全平方公式变形后,再利用基本不等式即可求出
的值代入,利用完全平方公式变形后,再利用基本不等式即可求出 的最大值.
的最大值.
试题解析:(1)
 , 3分
, 3分
所以函数的最小正周期为 . 4分
. 4分
由 得
得
所以函数的单调递增区间为 . 6分
. 6分
(2)由 可得
可得 ,又
,又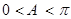 ,所以
,所以 。8分
。8分
由余弦定理可得 ,即
,即 又
又 ,所以
,所以 ,故
,故 ,当且仅当
,当且仅当 ,即
,即 时等号成立
时等号成立
因此 的最大值为
的最大值为 . 12分
. 12分
考点:解三角形;三角函数的化简求值;三角函数的周期性及其求法;正弦函数的单调性.


科目:高中数学 来源: 题型:解答题
函数f(x)=Asin  +1(A>0,ω>0)的最大值为3,其图象相邻两条对称轴之间的距离为
+1(A>0,ω>0)的最大值为3,其图象相邻两条对称轴之间的距离为 .
.
(1)求函数f(x)的解析式;
(2)设α∈ ,f
,f =2,求α的值.
=2,求α的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设向量a=(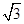 sin x,sin x),b=(cos x,sin x),x∈
sin x,sin x),b=(cos x,sin x),x∈ .
.
(1)若|a|=|b|,求x的值;
(2)设函数f(x)=a·b,求f(x)的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=2sin ωx·cos ωx+2 cos2ωx-
cos2ωx- (其中ω>0),且函数f(x)的周期为π.
(其中ω>0),且函数f(x)的周期为π.
(1)求ω的值;
(2)将函数y=f(x)的图象向右平移 个单位长度,再将所得图象各点的横坐标缩小到原来的
个单位长度,再将所得图象各点的横坐标缩小到原来的 倍(纵坐标不变)得到函数y=g(x)的图象,求函数g(x)在
倍(纵坐标不变)得到函数y=g(x)的图象,求函数g(x)在 上的单调区间.
上的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)= sin ωx-sin2
sin ωx-sin2 +
+ (ω>0)的最小正周期为π.
(ω>0)的最小正周期为π.
(1)求ω的值及函数f(x)的单调递增区间;
(2)当x∈ 时,求函数f(x)的取值范围.
时,求函数f(x)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 的周期为
的周期为 .
.
(1)若 ,求它的振幅、初相;
,求它的振幅、初相;
(2)在给定的平面直角坐标系中作出该函数在 的图像;
的图像;
(3)当 时,根据实数
时,根据实数 的不同取值,讨论函数
的不同取值,讨论函数 的零点个数.
的零点个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com