
分析 观察分子与多边形边的关系及分母中π的系数与多边形边的关系,即可得到答案
解答 解:在△ABC中,不等式$\frac{1}{A}$+$\frac{1}{B}$+$\frac{1}{C}$≥$\frac{9}{π}$成立;
在四边形ABCD中,不等式$\frac{1}{A}$+$\frac{1}{B}$+$\frac{1}{C}$+$\frac{1}{D}$≥$\frac{16}{2π}$成成立;
在五边形ABCDE中,不等式$\frac{1}{A}$+$\frac{1}{B}$+$\frac{1}{C}$+$\frac{1}{D}$+$\frac{1}{E}$≥$\frac{25}{3π}$成立.
…
归纳可得:在n边形A1A2A3…An中,$\frac{1}{A_1}+\frac{1}{A_2}+\frac{1}{A_3}+…+\frac{1}{A_n}≥\frac{n^2}{(n-2)π}$;
故答案为:$\frac{1}{A_1}+\frac{1}{A_2}+\frac{1}{A_3}+…+\frac{1}{A_n}≥\frac{n^2}{(n-2)π}$;
点评 本题考查归纳推理,考查不等式的证明,其中根据已知分析分子与多边形边的关系及分母中π的系数与多边形边的关系,是解答本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $?m∈[{0,1}],x+\frac{1}{x}<{2^m}$ | B. | $?m∈[{0,1}],x+\frac{1}{x}≥{2^m}$ | C. | $?m∈[{0,1}],x+\frac{1}{x}≤{2^m}$ | D. | $?m∈[{0,1}],x+\frac{1}{x}<{2^m}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
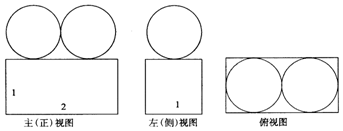
| A. | 2+$\frac{4π}{3}$ | B. | 2+$\frac{π}{3}$ | C. | 1+$\frac{4π}{3}$ | D. | 10+8π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 数据 | 31,12,22,15,20,45,47,32,34,23,28 |
| A. | 23、32 | B. | 34、35 | C. | 28、32 | D. | 28、35 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
| 年份代号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com