
分析 先画出正切函数的图象,根据图象和题意列出不等式,求出x的取值范围.
解答 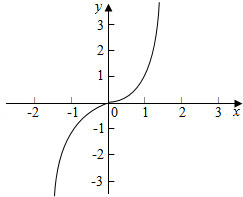 解:画出正切函数的图象如图:
解:画出正切函数的图象如图:
因为tan(x-$\frac{π}{3}$)>1,
所以kπ+$\frac{π}{4}$<x-$\frac{π}{3}$<kπ+$\frac{π}{2}$(k∈Z),
解得kπ+$\frac{7π}{12}$<x-$\frac{π}{3}$<kπ+$\frac{5π}{6}$(k∈Z),
所以x的取值范围是$(kπ+\frac{7π}{12},kπ+\frac{5π}{6})$(k∈Z),
故答案为:$(kπ+\frac{7π}{12},kπ+\frac{5π}{6})$(k∈Z).
点评 本题考查利用正切函数的图象解不等式,考查数形结合思想,整体思想,属于中档题.


科目:高中数学 来源: 题型:解答题
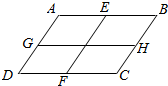 已知E,F,G,H分别是四边形ABCD四条边AB,CD,AD,BC的中点,求$\overrightarrow{AB}$+$\overrightarrow{BC}$+$\overrightarrow{AD}$+$\overrightarrow{DC}$=2($\overrightarrow{EF}$+$\overrightarrow{GH}$)
已知E,F,G,H分别是四边形ABCD四条边AB,CD,AD,BC的中点,求$\overrightarrow{AB}$+$\overrightarrow{BC}$+$\overrightarrow{AD}$+$\overrightarrow{DC}$=2($\overrightarrow{EF}$+$\overrightarrow{GH}$)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x-2)2+(y+3)2=2 | B. | (x+2)2+(y-3)2=2 | C. | (x+2)2+(y-3)2=8 | D. | (x-2)2+(y+3)2=8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com