
分析 (1)直接运用点到直线的距离公式,然后求解即可得到答案.
(2)属于新定义的题目,可以用函数求导数求最值的方法解答.
解答 解:(1)因为f(x)=a2x2,所以f′(x)=2a2x,
令f′(x)=2a2x=1
得:x=$\frac{1}{2{a}^{2}}$,
此时y=$\frac{1}{4{a}^{2}}$,
则点($\frac{1}{2{a}^{2}}$,$\frac{1}{4{a}^{2}}$)到直线x-y-3=0的距离为2$\sqrt{2}$,
即$\frac{|\frac{1}{2{a}^{2}}-\frac{1}{4{a}^{2}}-3|}{\sqrt{2}}$=2$\sqrt{2}$,
解之得a=$\frac{\sqrt{7}}{14}$;
(2)设F(x)=f(x)-g(x)=$\frac{1}{2}$x2-elnx,
则F′(x)=x-$\frac{e}{x}$,
所以当0<x<$\sqrt{e}$时,F′(x)<0;当x>$\sqrt{e}$时,F′(x)>0.
因此x=$\sqrt{e}$时,F(x)取得最小值0,
则f(x)与g(x)的图象在x=$\sqrt{e}$处有公共点($\sqrt{e}$,$\frac{1}{2}$e).
设f(x)与g(x)存在“分界线”,
方程为y-$\frac{1}{2}$e=k(x-$\sqrt{e}$),即y=kx+$\frac{1}{2}$e-k$\sqrt{e}$,
由f(x)≥kx+$\frac{1}{2}$e-k$\sqrt{e}$在x∈R恒成立,
则x2-2kx-e+2k$\sqrt{e}$≥0在x∈R恒成立.
所以△=4k2-4(2k$\sqrt{e}$-e)=4k2-8k$\sqrt{e}$+4e=4(k-$\sqrt{e}$)2≤0成立,
因此k=$\sqrt{e}$.
下面证明g(x)≤$\sqrt{e}$x-$\frac{1}{2}$e(x>0)恒成立.
设G(x)=elnx-x$\sqrt{e}$+$\frac{1}{2}$e(x>0),
则G′(x)=$\frac{e}{x}$-$\sqrt{e}$=$\frac{\sqrt{e}(\sqrt{e}-x)}{x}$.
所以当0<x<$\sqrt{e}$时,G′(x)>0;当x>$\sqrt{e}$时,G′(x)<0.
因此x=$\sqrt{e}$时G(x)取得最大值0,则g(x)≤$\sqrt{e}$x-$\frac{1}{2}$e成立.
故所求“分界线”方程为:y=$\sqrt{e}$x-$\frac{1}{2}$e.
点评 此题主要考查点到直线距离公式的应用及利用导函数求闭区间极值问题,题中涉及到新定义的问题,此类型的题目需要仔细分析再求解,综合性较强,有一定的技巧性,属于难题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | 3 | D. | -3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
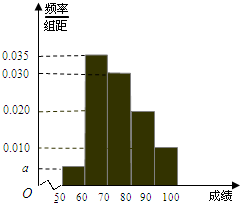 某校100名学生期中考试数学成绩的频率分布直方图如图,其中成绩分组区间如下:
某校100名学生期中考试数学成绩的频率分布直方图如图,其中成绩分组区间如下:| 组号 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 |
| 分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | cos(2x-1) | B. | -2cos(2x-1) | C. | 2cos(2x-1) | D. | -cos(2x-1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com