Question

【题目】已知函数.

（1）讨论函数的单调性；

（2）设函数图象上不重合的两点.证明：.（是直线的斜率）

Answer 1

【答案】（1）①当时，函数在上单调递增；②当时，函数在上单调递增，在上单调递减.（2）证明见解析

【解析】

（1）先由题意，得到函数定义域，对函数求导，分别讨论和两种情况，解对应的不等式，即可得出其单调性；

（2）根据斜率公式，由题意，得到，再由，将证明的问题转化为证明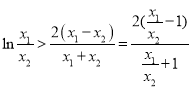，令，即证时，成立，设，对其求导，用导数的方法求其范围，即可得出结果.

（1）函数的定义域为，

且

①当时，，此时在单调递增；

②当时，令可得或（舍），，

由得，由得，

所以在上单调递增，在上单调递减.

综上：①当时，函数在上单调递增；

②当时，函数在上单调递增，在上单调递减.

（2）由题意得，

所以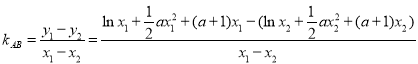

又，

要证成立，

即证：成立，

即证：成立.

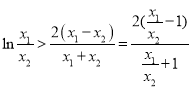令，即证时，成立.

设

则

所以函数在上是增函数，

所以，都有，

即，，

所以