
【题目】设等差数列![]() 的公差d大于0,前n项的和为
的公差d大于0,前n项的和为![]() .已知
.已知![]() =18,
=18,![]() ,
,![]() ,
,![]() 成等比数列.
成等比数列.
(1)求![]() 的通项公式;
的通项公式;
(2)若对任意的![]() ,都有k(
,都有k(![]() +18)≥
+18)≥![]() 恒成立,求实数k的取值范围;
恒成立,求实数k的取值范围;
(3)设![]() (
(![]() ).若s,t
).若s,t![]() ,s>t>1,且
,s>t>1,且![]() ,求s,t的值.
,求s,t的值.
【答案】(2)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)结合等比中项的性质列方程,将已知条件转化为![]() 的形式列方程组,解方程组求得
的形式列方程组,解方程组求得![]() ,由此求得
,由此求得![]() 的通项公式.
的通项公式.
(2)由(1)求得![]() ,将不等式
,将不等式![]() 分离常数
分离常数![]() ,利用换元法,结合基本不等式,求得
,利用换元法,结合基本不等式,求得![]() 的取值范围.
的取值范围.
(3)求得![]() 的表达式,利用
的表达式,利用![]() 判断出数列
判断出数列![]() 的项的大小关系,由此确定
的项的大小关系,由此确定![]() 的值.
的值.
(1)由于![]() 成等比数列,所以
成等比数列,所以![]() ,依题意有
,依题意有 ,由于
,由于![]() ,故方程组解得
,故方程组解得![]() ,所以
,所以![]() .即
.即![]() 的通项公式为
的通项公式为![]() .
.
(2)由(1)得![]() ,由于对任意的
,由于对任意的![]() ,都有
,都有![]() 恒成立,所以
恒成立,所以![]() 对任意的
对任意的![]() 恒成立.
恒成立.
设![]() ,令
,令![]() ,则
,则
![]() .因为
.因为![]() ,当且仅当
,当且仅当![]() 时等号成立,所以
时等号成立,所以![]() 的最大值为
的最大值为![]() ,即
,即![]() 的最大值为
的最大值为![]() ,此时
,此时![]() ,所以实数
,所以实数![]() 的取值范围是
的取值范围是![]() .
.
(3)由条件,![]() ,则
,则![]()
![]() ,所以
,所以![]() .因为
.因为![]() ,所以
,所以![]() .即符合条件的
.即符合条件的![]() 的值分别为
的值分别为![]() .
.


科目:高中数学 来源: 题型:
【题目】给定数列![]() ,对
,对![]() ,该数列前
,该数列前![]() 项的最大值记为
项的最大值记为![]() ,后
,后![]() 项
项![]() 的最小值记为
的最小值记为![]() ,
,![]() .
.
(1)设数列![]() 为3,4,7,5,2,写出
为3,4,7,5,2,写出![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)设![]() 是
是![]() ,公比
,公比![]() 的等比数列,证明:
的等比数列,证明:![]() 成等比数列;
成等比数列;
(3)设![]() ,证明:
,证明:![]() 的充分必要条件为
的充分必要条件为![]() 是公差为
是公差为![]() 的等差数列.
的等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,侧面
中,侧面![]() 底面ABC,
底面ABC,![]()
![]() ,且
,且![]() ,O为AC中点.
,O为AC中点.

(1)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(2)在![]() 上是否存在一点E,使得
上是否存在一点E,使得![]() 平面
平面![]() ,若不存在,说明理由;若存在,确定点E的位置.
,若不存在,说明理由;若存在,确定点E的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线C:![]() ,则( )
,则( )
A.双曲线C的离心率等于半焦距的长
B.双曲线![]() 与双曲线C有相同的渐近线
与双曲线C有相同的渐近线
C.双曲线C的一条准线被圆x2+y2=1截得的弦长为![]()
D.直线y=kx+b(k,b![]() R)与双曲线C的公共点个数只可能为0,1,2
R)与双曲线C的公共点个数只可能为0,1,2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某社区有居民![]() 人,为了迎接第十一个“全民健身日”的到来,居委会从中随机抽取了
人,为了迎接第十一个“全民健身日”的到来,居委会从中随机抽取了![]() 名居民,统计了他们本月参加户外运动时间(单位:小时)的数据,并将数据进行整理,分为
名居民,统计了他们本月参加户外运动时间(单位:小时)的数据,并将数据进行整理,分为![]() 组:
组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.
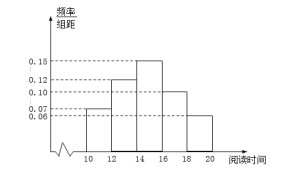
(Ⅰ)试估计该社区所有居民中,本月户外运动时间不小于![]() 小时的人数;
小时的人数;
(Ⅱ)已知这![]() 名居民中恰有
名居民中恰有![]() 名女性的户外运动时间在
名女性的户外运动时间在![]() ,现从户外运动时间在
,现从户外运动时间在![]() 的样本对应的居民中随机抽取
的样本对应的居民中随机抽取![]() 人,求至少抽到
人,求至少抽到![]() 名女性的概率.
名女性的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一只昆虫的产卵数![]() 与温度
与温度![]() 有关,现收集了6组观测数据与下表中.由散点图可以发现样本点分布在某一指数函数曲线
有关,现收集了6组观测数据与下表中.由散点图可以发现样本点分布在某一指数函数曲线![]() 的周围.
的周围.
温度 | 21 | 23 | 25 | 27 | 29 | 31 |
产卵数 | 7 | 11 | 21 | 24 | 66 | 114 |
令![]() ,经计算有:
,经计算有:
|
|
|
|
|
|
26 | 40.5 | 19.50 | 6928 | 526.60 | 70 |
(1)试建立![]() 关于
关于![]() 的回归直线方程并写出
的回归直线方程并写出![]() 关于
关于![]() 的回归方程
的回归方程![]() .
.
(2)若通过人工培育且培育成本![]() 与温度
与温度![]() 和产卵数
和产卵数![]() 的关系为
的关系为![]() (单位:万元),则当温度为多少时,培育成本最小?
(单位:万元),则当温度为多少时,培育成本最小?
注:对于一组具有线性相关关系的数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘公式分别为
的斜率和截距的最小二乘公式分别为 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com