
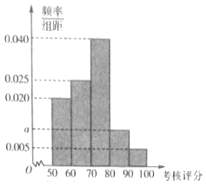
 2016年,某省环保部门制定了《省工业企业环境保护标准化建设基本要求及考核评分标准》,为了解本省各家企业对环保的重视情况,从中抽取了40家企业进行考核评分,考核评分均在[50,100]内,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图如图(满分为100分).
2016年,某省环保部门制定了《省工业企业环境保护标准化建设基本要求及考核评分标准》,为了解本省各家企业对环保的重视情况,从中抽取了40家企业进行考核评分,考核评分均在[50,100]内,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图如图(满分为100分).分析 (I)由频率分布直方图可得:(0.020+0.025+0.040+a+0.005)×10=1,解得a.即可得出估计该省在2016年对这40家企业投放环保奖励的平均值.
(II)在区间[80,90)有4家,在区间[90,100)有2家.X的可能取值为1,2,3.P(X=k)=$\frac{{∁}_{4}^{k}{∁}_{2}^{3-k}}{{∁}_{6}^{3}}$,即可得出其分布列与数学期望.
解答 解:(I)由频率分布直方图可得:(0.020+0.025+0.040+a+0.005)×10=1,解得a=0.01.
∴估计该省在2016年对这40家企业投放环保奖励的平均值=-7×0.020×10+0×0.025×10+3×0.040×10+6×(0.01+0.005)×10=0.7(万元).
(II)在区间[80,90)有4家,在区间[90,100)有2家.X的可能取值为1,2,3.
P(X=k)=$\frac{{∁}_{4}^{k}{∁}_{2}^{3-k}}{{∁}_{6}^{3}}$,P(X=1)=$\frac{4}{20}$=$\frac{1}{5}$,P(X=2)=$\frac{12}{20}$=$\frac{3}{5}$,P(X=3)=$\frac{4}{20}$=$\frac{1}{5}$.
可得X的分布列如下:
| X | 1 | 2 | 3 |
| P | $\frac{1}{5}$ | $\frac{3}{5}$ | $\frac{1}{5}$ |
点评 本题考查了频率分布直方图的性质、超几何分布列的性质及其数学期望,考查了推理能力与计算能力,属于中档题.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{2}$ | B. | $\frac{5}{3}$ | C. | $\frac{5}{4}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
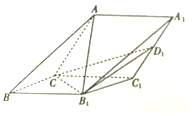 如图,在三棱锥ABC-A1B1C1中,侧面ACC1A1与侧面CBB1C1都是菱形,∠ACC1=∠CC1B1=60°,AC=2$\sqrt{3}$.
如图,在三棱锥ABC-A1B1C1中,侧面ACC1A1与侧面CBB1C1都是菱形,∠ACC1=∠CC1B1=60°,AC=2$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 明天该地区约有80%的时间会下雨,20%的时间不下雨 | |
| B. | 明天该地区约有80%的地方会下雨,20%的地方不下雨 | |
| C. | 明天该地区下雨的可能性为80% | |
| D. | 该地区约有80%的人认为明天会下雨,20%的人认为明天不下雨 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{\frac{π}{4},\frac{π}{3}}]$ | B. | $[{-\frac{π}{6},\frac{π}{4}}]$ | C. | $[{\frac{π}{6},\frac{π}{4}}]$ | D. | $({\frac{π}{6},\frac{π}{2}}]$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com