
分析 (Ⅰ)由椭圆的定义可知:动点A的轨迹的轨迹为为以B,C为焦点的椭圆(y≠0),则c=1,a=2,b=$\sqrt{3}$,即可求得椭圆方程;
(Ⅱ)分别求得PB及BC的垂直平分线,联立,由P在椭圆上,$y=\frac{3}{{2{y_0}}}-\frac{y_0}{6}$,利用点到直线的距离公式,根据函数的单调性即可求得O1到x轴的距离的最小值.
解答 解:(Ⅰ)根据题意知,动点A满足椭圆的定义,(1分)
设椭圆的方程$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0,且y≠0),
所以,有|F1F2|=|BC|=2c=2,|AF1|+|AF2|=|AB|+|AC|=2a=4,(2分)
且a2=b2+c2解得$a=2,b=\sqrt{3}$(3分)
所以,动点A的轨迹C满足的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1,(y≠0)$(4分)
没有写出约束条件的扣(1分)
(Ⅱ)设P(x0,y0),不妨设$0<{y_0}≤\sqrt{3}$
线段PB的垂直平分线方程为$y-\frac{y_0}{2}=-\frac{{{x_0}+1}}{y_0}(x-\frac{{{x_0}-1}}{2})$(6分)
线段BC的垂直平分线方程为x=0,两条垂线方程联立求得
$y=(-\frac{{{x_0}+1}}{y_0})(-\frac{{{x_0}-1}}{2})+\frac{y_0}{2}=\frac{x_0^2-1}{{2{y_0}}}+\frac{y_0}{2}$(8分)
∵$\frac{x_0^2}{4}+\frac{y_0^2}{3}=1$∴$y=\frac{3}{{2{y_0}}}-\frac{y_0}{6}$(9分)
∴⊙O1的圆心O1到x轴的距离$d=|{\frac{3}{{2{y_0}}}-\frac{y_0}{6}}|$(10分)
又知$y=\frac{3}{{2{y_0}}}-\frac{y_0}{6}$在$(0,\sqrt{3})$上是单调递减函数
∴当${y_0}=\sqrt{3}$时,${y_{min}}=\frac{{\sqrt{3}}}{3}$,
∴${d_{min}}=\frac{{\sqrt{3}}}{3}$(12分)
点评 本题考查椭圆的定义,直线的垂直平分线的求法,函数单调性与椭圆的应用,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+i | B. | -1+i | C. | 1-i | D. | -1-i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2017}$ | B. | $\frac{1}{2016}$ | C. | $\frac{2016}{2017}$ | D. | $\frac{2015}{2016}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | (-7,-4] | C. | (-7,4] | D. | [-4,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a=-1,b=-2 | B. | a=-1,b=2 | C. | a=1,b=2 | D. | a=1,b=-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
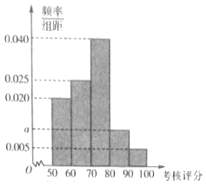 2016年,某省环保部门制定了《省工业企业环境保护标准化建设基本要求及考核评分标准》,为了解本省各家企业对环保的重视情况,从中抽取了40家企业进行考核评分,考核评分均在[50,100]内,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图如图(满分为100分).
2016年,某省环保部门制定了《省工业企业环境保护标准化建设基本要求及考核评分标准》,为了解本省各家企业对环保的重视情况,从中抽取了40家企业进行考核评分,考核评分均在[50,100]内,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图如图(满分为100分).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com