
| A. | $[{\frac{π}{4},\frac{π}{3}}]$ | B. | $[{-\frac{π}{6},\frac{π}{4}}]$ | C. | $[{\frac{π}{6},\frac{π}{4}}]$ | D. | $({\frac{π}{6},\frac{π}{2}}]$ |
分析 由题意可得y=sin(ωx+φ)的图象和直线y=$\frac{1}{2}$ 的相邻的两个交点间的距离为$\frac{π}{3}$,∴可得$\frac{1}{3}•\frac{2π}{ω}$=$\frac{π}{3}$,求得ω=2,可得f(x)=2sin(2x+φ)+1.
根据当x∈(-$\frac{π}{8}$,$\frac{π}{3}$) 时,sin(2x+φ)>0,可得2•(-$\frac{π}{8}$)+φ≥2kπ,2•$\frac{π}{3}$+φ≤2kπ+π,k∈Z,求得 φ的范围.
解答 解:∵函数f(x)=2sin(ωx+φ)+1(ω>0,|φ|≤$\frac{π}{2}}$),其图象与直线y=2最近的两个相邻交点间的距离为$\frac{π}{3}$,
令2sin(ωx+φ)+1=2,求得sin(ωx+φ)=$\frac{1}{2}$,y=sin(ωx+φ)的图象和直线y=$\frac{1}{2}$ 的相邻的两个交点间的距离为$\frac{π}{3}$,
∴$\frac{1}{3}•\frac{2π}{ω}$=$\frac{π}{3}$,∴ω=2,f(x)=2sin(2x+φ)+1.
∵f(x)>1对$?x∈({-\frac{π}{8},\frac{π}{3}})$恒成立,∴当x∈(-$\frac{π}{8}$,$\frac{π}{3}$) 时,2sin(2x+φ)+1>1恒成立,即sin(2x+φ)>0,
∴2•(-$\frac{π}{8}$)+φ≥2kπ,2•$\frac{π}{3}$+φ≤2kπ+π,k∈Z,求得 φ≥2kπ+$\frac{π}{4}$,且φ≤2kπ+$\frac{π}{3}$,k∈Z,
即φ∈[2kπ+$\frac{π}{4}$,2kπ+$\frac{π}{3}$],
故选:A.
点评 本题主要考查正弦函数的图象和性质,函数的恒成立问题,属于中档题.


科目:高中数学 来源: 题型:解答题
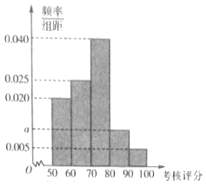 2016年,某省环保部门制定了《省工业企业环境保护标准化建设基本要求及考核评分标准》,为了解本省各家企业对环保的重视情况,从中抽取了40家企业进行考核评分,考核评分均在[50,100]内,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图如图(满分为100分).
2016年,某省环保部门制定了《省工业企业环境保护标准化建设基本要求及考核评分标准》,为了解本省各家企业对环保的重视情况,从中抽取了40家企业进行考核评分,考核评分均在[50,100]内,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图如图(满分为100分).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 33 | B. | 35 | C. | 37 | D. | 39 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
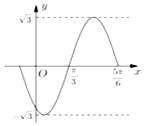 如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π),x∈R的部分图象,则下列命题中,正确的命题序号是( )
如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π),x∈R的部分图象,则下列命题中,正确的命题序号是( )| A. | ③⑤ | B. | ③④ | C. | ④⑤ | D. | ①③ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{41}{26}$ | B. | $\frac{23}{14}$ | C. | $\frac{11}{7}$ | D. | $\frac{11}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -x2-2sinx | B. | -x2+2sinx | C. | x2+2sinx | D. | x2-2sinx |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com