
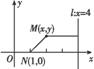
已知动点M(x,y)到直线l:x=4的距离是它到点N(1,0)的距离的2倍.
(1)求动点M的轨迹C的方程;
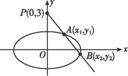
(2)过点P(0,3)的直线m与轨迹C交于A,B两点,若A是PB的中点,求直线m的斜率.
解:(1)设M到直线l的距离为d,
根据题意,d=2|MN|.
由此得|4-x|=2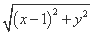 ,
,
化简得 +
+ =1,
=1,
所以,动点M的轨迹方程为 +
+ =1.
=1.
(2)法一 由题意,设直线m的方程为y=kx+3,A(x1,y1),B(x2,y2).
将y=kx+3代入 +
+ =1中,
=1中,
有(3+4k2)x2+24kx+24=0,
其中,Δ=(24k)2-4×24(3+4k2)=96(2k2-3)>0,
由求根公式得,
x1+x2=-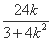 , ①
, ①
x1x2=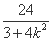 . ②
. ②
又因A是PB的中点,
故x2=2x1,③
将③代入①,②,得
x1=-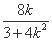 ,
,
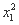 =
=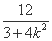 ,
,
可得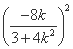 =
=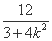 ,
,
且k2> ,
,
解得k=- 或k=
或k= ,
,
所以,直线m的斜率为- 或
或 .
.
法二 由题意,设直线m的方程为y=kx+3,
A(x1,y1),B(x2,y2).
∵A是PB的中点,
∴x1=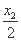 ,①
,①
y1=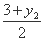 .②
.②
又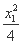 +
+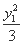 =1,③
=1,③
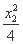 +
+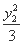 =1.④
=1.④
联立①,②,③,④解得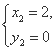 或
或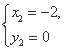
即点B的坐标为(2,0)或(-2,0),
所以,直线m的斜率为- 或
或 .
.


科目:高中数学 来源: 题型:
设F1,F2是椭圆E:  +
+ =1(a>b>0)的左、右焦点,P为直线x=
=1(a>b>0)的左、右焦点,P为直线x= 上一点,△F2PF1是底角为30°的等腰三角形,则E的离心率为( )
上一点,△F2PF1是底角为30°的等腰三角形,则E的离心率为( )
(A) (B)
(B) (C)
(C) (D)
(D) 
查看答案和解析>>
科目:高中数学 来源: 题型:
已知椭圆 +
+ =1(a>b>0),点P(
=1(a>b>0),点P( a,
a, a)在椭圆上.
a)在椭圆上.
(1)求椭圆的离心率;
(2)设A为椭圆的左顶点,O为坐标原点,若点Q在椭圆上且满足|AQ|=|AO|,求直线OQ的斜率的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
在平面直角坐标系xOy中,F是抛物线C:x2=2py(p>0)的焦点,M是抛物线C上位于第一象限内的任意一点,过M,F,O三点的圆的圆心为Q,点Q到抛物线C的准线的距离为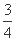 .
.
(1)求抛物线C的方程;
(2)是否存在点M,使得直线MQ与抛物线C相切于点M?若存在,求出点M的坐标;若不存在,说明理由.
(3)若点M的横坐标为 ,直线l:y=kx+
,直线l:y=kx+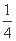 与抛物线C有两个不同的交点A,B,l与圆Q有两个不同的交点D,E,求当
与抛物线C有两个不同的交点A,B,l与圆Q有两个不同的交点D,E,求当 ≤k≤2时,|AB|2+|DE|2的最小值.
≤k≤2时,|AB|2+|DE|2的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
某商场有来自三个国家的进口奶制品,其中A国、B国、C国的奶制品分别有40种、10种、30种,现从中抽取一个容量为16的样本进行三聚氰胺检测,若采用分层抽样的方法抽取样本,则抽取来自B国的奶制品________种.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com