
��ƽ��ֱ������ϵxOy��,F��������C:x2=2py(p>0)�Ľ���,M��������C��λ�ڵ�һ�����ڵ�����һ��,��M,F,O�����Բ��Բ��ΪQ,��Q��������C���ߵľ���Ϊ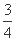 .
.
(1)��������C�ķ���;
(2)�Ƿ���ڵ�M,ʹ��ֱ��MQ��������C�����ڵ�M?������,�����M������;��������,˵������.
(3)����M�ĺ�����Ϊ ,ֱ��l:y=kx+
,ֱ��l:y=kx+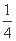 ��������C��������ͬ�Ľ���A,B,l��ԲQ��������ͬ�Ľ���D,E,��
��������C��������ͬ�Ľ���A,B,l��ԲQ��������ͬ�Ľ���D,E,�� ��k��2ʱ,|AB|2+|DE|2����Сֵ.
��k��2ʱ,|AB|2+|DE|2����Сֵ.
��:(1)������֪F ,Բ��Q���߶�OF�Ĵ�ֱƽ����y=
,Բ��Q���߶�OF�Ĵ�ֱƽ����y=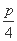 ��,
��,
��Ϊ������C���߷���Ϊy=-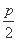 ,
,
����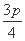 =
=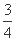 ,
,
��p=1.
���������C�ķ���Ϊx2=2y.
(2)������ڵ�M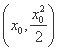 (x0>0)��������,������C�ڵ�M��������б��Ϊy��
(x0>0)��������,������C�ڵ�M��������б��Ϊy��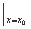 =
=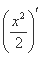
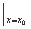 =x0,
=x0,
����ֱ��MQ�ķ���Ϊy-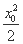 =x0(x-x0).
=x0(x-x0).
��y=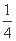 ��xQ=
��xQ=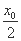 +
+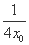 .
.
����Q��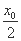 +
+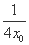 ,
,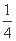 ��.
��.
��|QM|=|OQ|,
�ʣ�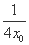 -
-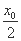 ��2+��
��2+��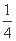 -
-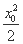 ��2=��
��2=��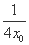 +
+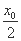 ��2+
��2+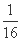 ,
,
��ˣ�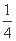 -
-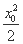 ��2=
��2= .
.
��x0>0,
����x0= ,��ʱM(
,��ʱM( ,1).
,1).
�ʴ��ڵ�M( ,1),
,1),
ʹ��ֱ��MQ��������C�����ڵ�M.
(3)��x0= ʱ,��(2)��Q��
ʱ,��(2)��Q�� ,
,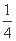 ��,
��,
��Q�İ뾶Ϊr=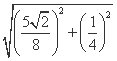 =
=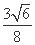 ,
,
���Ԩ�Q�ķ���Ϊ��x- ��2+��y-
��2+��y-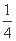 ��2=
��2=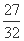 .
.
��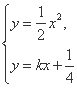
������2x2-4kx-1=0.
��A,B���������ֱ�Ϊ(x1,y1),(x2,y2),
���ڦ�1=16k2+8>0,x1+x2=2k,x1x2=- ,
,
����|AB|2=(1+k2)[(x1+x2)2-4x1x2]
=(1+k2)(4k2+2).
��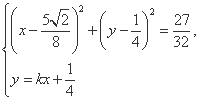
������(1+k2)x2-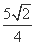 x-
x-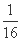 =0.
=0.
��D,E���������ֱ�Ϊ(x3,y3),(x4,y4),
���ڦ�2=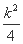 +
+ >0,x3+x4=
>0,x3+x4=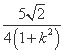 ,
,
x3x4=-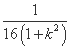 .
.
����|DE|2=(1+k2)[(x3+x4)2-4x3x4]
=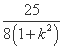 +
+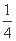 .
.
���|AB|2+|DE|2=(1+k2)(4k2+2)+ 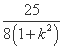 +
+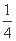 .
.
��1+k2=t,
���� ��k��2,
��k��2,
�� ��t��5,
��t��5,
����|AB|2+|DE|2=t(4t-2)+  +
+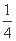
=4t2-2t+ +
+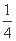 ,
,
��g(t)=4t2-2t+ +
+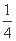 ,t��
,t��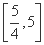 ,
,
��Ϊg��(t)=8t-2-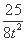 ,
,
���Ե�t��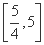 ʱ,g��(t)��g��
ʱ,g��(t)��g�� =6,
=6,
������g(t)��t��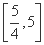 ����������,
����������,
���Ե�t= ʱ,g(t)ȡ����Сֵ
ʱ,g(t)ȡ����Сֵ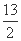 ,
,
���,��k= ʱ,|AB|2+|DE|2ȡ����Сֵ
ʱ,|AB|2+|DE|2ȡ����Сֵ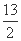 .
.


 ��Ȥ����¹�֪��ϵ�д�
��Ȥ����¹�֪��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
��֪����M(x,y)��ֱ��l:x=4�ľ�����������N(1,0)�ľ����2��.
(1)��M�Ĺ켣C�ķ���;
(2)����P(0,3)��ֱ��m��켣C����A,B����,��A��PB���е�,��ֱ��m��б��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Բ +y2=1����ΪF,PΪ��Բ��һ��,�������Ϊ
+y2=1����ΪF,PΪ��Բ��һ��,�������Ϊ ,��|PF|����(����)
,��|PF|����(����)
(A) (B)
(B) (C)
(C) (D)
(D)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ,F1,F2����ԲC1: 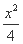 +y2=1��˫����C2�Ĺ�������,A,B�ֱ���C1,C2�ڵڶ��������Ĺ�����.���ı���AF1BF2Ϊ����,��C2����������(����)
+y2=1��˫����C2�Ĺ�������,A,B�ֱ���C1,C2�ڵڶ��������Ĺ�����.���ı���AF1BF2Ϊ����,��C2����������(����)
(A) (B)
(B) (C)
(C) (D)
(D)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
������C1:y= x2(p>0)�Ľ�����˫����C2:
x2(p>0)�Ľ�����˫����C2:  -y2=1���ҽ�������߽�C1�ڵ�һ���ĵ�M.��C1�ڵ�M��������ƽ����C2��һ��������,��p����(����)
-y2=1���ҽ�������߽�C1�ڵ�һ���ĵ�M.��C1�ڵ�M��������ƽ����C2��һ��������,��p����(����)
(A) (B)
(B) (C)
(C) (D)
(D)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��֪˫���� -
- =1(a>0,b>0)��һ�������߷�����y=
=1(a>0,b>0)��һ�������߷�����y= x,����һ��������������y2=16x�Ľ�����ͬ,��˫���ߵķ���Ϊ�� .
x,����һ��������������y2=16x�Ľ�����ͬ,��˫���ߵķ���Ϊ�� .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ��ʾ,��֪ԲC��y�������ڵ�T(0,2),��x���������ཻ������M,N(��M�ڵ�N���Ҳ�),��|MN|=3,��֪��ԲD:  +
+ =1(a>b>0)�Ľ������2|ON|,�ҹ��㣨
=1(a>b>0)�Ľ������2|ON|,�ҹ��㣨 ,
,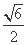 ��.
��.
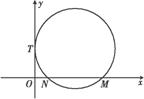
(1)��ԲC����ԲD�ķ���;
(2)������Mб�ʲ�Ϊ���ֱ��l����ԲD����A��B����,��֤:ֱ��NA��ֱ��NB����б�ǻ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
Ϊ�˽�ij��ѧ��ϲ���������Ƿ����Ա��йأ��Ըð�50��ѧ���������ʾ����飬�õ������µ�2��2��������
|
| ϲ�������� | ��ϲ�������� | �ϼ� |
| ���� | 20 | 5 | 25 |
| �� | 10 | 15 | 25 |
| �ϼ� | 30 | 20 | 50 |
��������________�İ�����Ϊϲ�����������Ա��йأ�(���ðٷ�����ʾ)
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com