
| |
认为作业多 | 认为作业不多 | 合计 |
| 喜欢玩游戏 | 18 | 9 | |
| 不喜欢玩游戏 | 8 | 15 | |
| 合计 |
| P(K2≥K0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| 认为作业多 | 认为作业不多 | 合计 | |
| 喜欢玩游戏 | 18 | 9 | 27 |
| 不喜欢玩游戏 | 8 | 15 | 23 |
| 合计 | 26 | 24 | 50 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| 50×?18×15-8×9?2 |
| 26×24×27×23 |


 名题金卷系列答案
名题金卷系列答案科目:高中数学 来源: 题型:
| 1 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、sin31°>cos59° |
| B、-cos59°>-cos61° |
| C、tan31°>tan61° |
| D、sin59°>cos59° |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
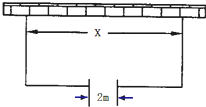 如图,围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的一扇门,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,一扇门的造价为600元,设利用的旧墙的长度为xm,总造价为y元.
如图,围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的一扇门,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,一扇门的造价为600元,设利用的旧墙的长度为xm,总造价为y元.查看答案和解析>>
科目:高中数学 来源: 题型:
 把所有正整数按上小下大,左小右大的原则排成如图所示的数表,其中第i行共有2i-1个正整数,设aij(i,j∈N*)表示位于这个数表中从上往下数第i行,从左往右第j个数.
把所有正整数按上小下大,左小右大的原则排成如图所示的数表,其中第i行共有2i-1个正整数,设aij(i,j∈N*)表示位于这个数表中从上往下数第i行,从左往右第j个数.| C | 3 n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com