
| π |
| 3 |
| 3 |
| π |
| 2 |
| a |
| c |
| a |
| c |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| a |
| c |
| sinA |
| sinC |
sin(
| ||
| sinC |
| ||
| 2tanC |
| 1 |
| 2 |
| 2π |
| 3 |
| π |
| 2 |
| π |
| 6 |
| π |
| 3 |
| ||
| 2tanC |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 1 |
| 2 |
| a |
| c |


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:
| 2 |
| 3 |
| A、135° | B、45° |
| C、135°或45° | D、90° |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 3 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
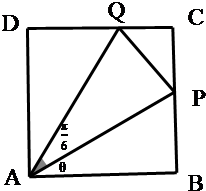 如图,某污水处理厂要在一正方形污水处理池ABCD内修建一个三角形隔离区以投放净化物质,其形状为三角形APQ,其中P位于边CB上,Q位于边CD上.已知AB=20米,∠PAQ=
如图,某污水处理厂要在一正方形污水处理池ABCD内修建一个三角形隔离区以投放净化物质,其形状为三角形APQ,其中P位于边CB上,Q位于边CD上.已知AB=20米,∠PAQ=| π |
| 6 |
| 正方形ABCD面积 |
| APAQ面积 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| |
认为作业多 | 认为作业不多 | 合计 |
| 喜欢玩游戏 | 18 | 9 | |
| 不喜欢玩游戏 | 8 | 15 | |
| 合计 |
| P(K2≥K0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
查看答案和解析>>
科目:高中数学 来源: 题型:
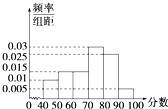 某校举行了由全部学生参加的校园安全知识考试,从中抽出60名学生,将其成绩分成六段[40,50),[50,60),…,[90,100]后,画出如图所示的频率分布直方图.观察图形的信息,回答下列问题:估计这次考试的及格率(60分及以上为及格)为
某校举行了由全部学生参加的校园安全知识考试,从中抽出60名学生,将其成绩分成六段[40,50),[50,60),…,[90,100]后,画出如图所示的频率分布直方图.观察图形的信息,回答下列问题:估计这次考试的及格率(60分及以上为及格)为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com