
| A. | $\frac{5}{14}$ | B. | $\frac{2}{7}$ | C. | $\frac{3}{14}$ | D. | $\frac{3}{28}$ |
分析 由题意可得 $\overrightarrow{OD}•\overrightarrow{AD}$=0,计算$\overrightarrow{OE}$•$\overrightarrow{EA}$=$\frac{\overrightarrow{OD}}{2}$•(-$\overrightarrow{AE}$)=$\frac{{|\overrightarrow{OD}|}^{2}}{4}$.△AOB中,利用余弦定理可得AB=$\sqrt{7}$,再利用面积法求得OD=$\frac{\sqrt{3}}{\sqrt{7}}$,从而求得$\overrightarrow{OE}$•$\overrightarrow{EA}$=$\frac{{|\overrightarrow{OD}|}^{2}}{4}$ 的值.
解答 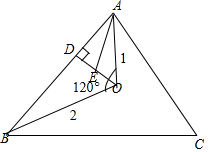 解:如图:点O为△ABC内一点,∠AOB=120°,OA=1,OB=2,
解:如图:点O为△ABC内一点,∠AOB=120°,OA=1,OB=2,
过O作OD垂直AB于点D,点E为线段OD的中点,∴$\overrightarrow{OD}•\overrightarrow{AD}$=0,
则$\overrightarrow{OE}$•$\overrightarrow{EA}$=$\frac{\overrightarrow{OD}}{2}$•(-$\overrightarrow{AE}$)=-$\frac{1}{2}$•$\overrightarrow{OD}$•$\frac{\overrightarrow{AO}+\overrightarrow{AD}}{2}$=-$\frac{\overrightarrow{AO}•\overrightarrow{OD}+\overrightarrow{OD}•\overrightarrow{AD}}{4}$
=$\frac{\overrightarrow{OA}•\overrightarrow{OD}}{4}$=$\frac{|\overrightarrow{OA}|•|\overrightarrow{OD}|•cos∠AOD}{4}$=$\frac{{|\overrightarrow{OD}|}^{2}}{4}$.
△AOB中,利用余弦定理可得AB2=OA2+OB2-2OA•OB•cos120°=1+4+2=7,∴AB=$\sqrt{7}$.
∵S△AOB=$\frac{1}{2}•AB•OD$=$\frac{1}{2}$OA•OB•sin120°,可得$\frac{1}{2}•\sqrt{7}$•OD=$\frac{1}{2}•1•2•\frac{\sqrt{3}}{2}$,
∴OD=$\frac{\sqrt{3}}{\sqrt{7}}$,∴$\overrightarrow{OE}$•$\overrightarrow{EA}$=$\frac{{|\overrightarrow{OD}|}^{2}}{4}$=$\frac{3}{28}$,
故选:D.
点评 本题主要考查两个向量的加减法的法则,以及其几何意义,两个向量的数量积的定义,属于中档题.


 优等生题库系列答案
优等生题库系列答案科目:高中数学 来源: 题型:解答题
| 甲组 | 乙组 | 合计 | |
| 男生 | 7 | 6 | |
| 女生 | 5 | 12 | |
| 合计 |
| P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,3} | B. | {2,4} | C. | {0,5} | D. | {0,1,2,3,4,5} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com