
分析 ①假设存在有穷常数列{c},它是好数列,则nc=0,解得c=0,而不满足$\sum_{k=1}^{n}$|ak|=1,即可判断出正误;
②例如:数列-$\frac{1}{2}$,0,$\frac{1}{2}$,是等差数列,为好数列,即可判断出正误.
③有穷等比数列{an}是2k阶好数列(k≥2),则必然q<0,由$\sum_{k=1}^{n}$ak=0,则a1×$\frac{1-{q}^{2k}}{1-q}$=0,解得q=-1.
④不可能存在各项非负的2013阶好数列,否则$\sum_{k=1}^{n}$ak=0不满足,即可判断出正误.
解答 解:①假设存在有穷常数列{c},它是好数列,则nc=0,解得c=0,而不满足$\sum_{k=1}^{n}$|ak|=1,因此不存在有穷常数列,它是好数列,正确.
②例如:数列-$\frac{1}{2}$,0,$\frac{1}{2}$,是等差数列,为好数列,正确.
③有穷等比数列{an}是2k阶好数列(k≥2),则必然q<0,由$\sum_{k=1}^{n}$ak=0,则a1×$\frac{1-{q}^{2k}}{1-q}$=0,解得q2k=1,则q=-1.
因此它的公比只能等于-l,正确;
④不可能存在各项非负的2013阶好数列,否则$\sum_{k=1}^{n}$ak=0不满足,因此不正确.
故答案为:①②③.
点评 本题考查了等差数列与等比数列的通项公式与求和公式、新定义,考查了推理能力与计算能力,属于难题.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 3x+4y-12=0或4x-3y+9=0 | B. | 3x+4y-12=0或x=0 | ||
| C. | 4x-3y+9=0或x=0 | D. | 3x-4y+12=0或4x+3y+9=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
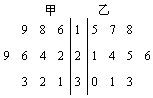 甲、乙两人在10天中每天加工零件的个数用茎叶图表示如图,中间一列的数字表示零件个数的十位数,两边的数字表示零件个数的个位数.则这十天甲、乙两人每人每日加工零件的平均数的和为49.
甲、乙两人在10天中每天加工零件的个数用茎叶图表示如图,中间一列的数字表示零件个数的十位数,两边的数字表示零件个数的个位数.则这十天甲、乙两人每人每日加工零件的平均数的和为49.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{28}{3}$ | B. | $\frac{19}{2}$ | C. | 6 | D. | 2$\sqrt{10}$+3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{18}{35}$ | B. | $\frac{15}{35}$ | C. | $\frac{12}{35}$ | D. | $\frac{9}{35}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
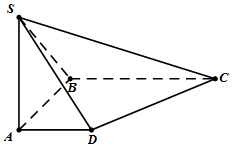 已知四棱锥S-ABCD中,四边形ABCD是直角梯形,∠ABC=∠BAD=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=$\frac{1}{2}$.
已知四棱锥S-ABCD中,四边形ABCD是直角梯形,∠ABC=∠BAD=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[-\frac{5π}{6},\frac{7π}{6}]$ | B. | $[\frac{7π}{6},\frac{19π}{6}]$ | C. | $[-\frac{2π}{3},\frac{4π}{3}]$ | D. | $[-\frac{17π}{6},-\frac{5π}{6}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 120° | B. | 60° | C. | 45° | D. | 30° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com