
| A. | 偶函数,奇函数 | B. | 奇函数,偶函数 | C. | 偶函数,偶函数 | D. | 奇函数,奇函数 |
分析 直接运用奇偶性的定义判断f(x)的奇偶性,在用分类讨论的办法确定g(x)的奇偶性,进而得到结果.
解答 解:先考察f(x)=|x-a|+|x+a|,
f(-x)=|-x-a|+|-x+a|=|x+a|+|x-a|=f(x),
即f(-x)=f(x),所以f(x)为偶函数;
再考察$g(x)=\left\{\begin{array}{l}-{x^2}+x,({x>0})\\{x^2}+x,({x≤0})\end{array}\right.$,
①当x>0时,g(x)=-x2+x,
所以-x<0,g(-x)=(-x)2+(-x)=x2-x=-(-x2+x)=-g(x),
②当x<0时,也满足g(-x)=-g(x),
且g(0)=0,所以,g(x)为R上的奇函数,
即f(x)为偶函数,g(x)为奇函数,
故答案为:A.
点评 本题主要考查了运用奇偶性的定义判断函数的奇偶性,涉及绝对值函数和分段函数奇偶性的判断,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
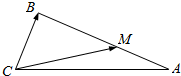 如图,在△ABC中,|$\overrightarrow{CA}$|=6,|$\overrightarrow{CB}$|=3,M为线段AB上的一点,且|$\overrightarrow{CM}$|=x•$\overrightarrow{CA}$+y•$\overrightarrow{CB}$,$\overrightarrow{BM}$=2$\overrightarrow{MA}$.
如图,在△ABC中,|$\overrightarrow{CA}$|=6,|$\overrightarrow{CB}$|=3,M为线段AB上的一点,且|$\overrightarrow{CM}$|=x•$\overrightarrow{CA}$+y•$\overrightarrow{CB}$,$\overrightarrow{BM}$=2$\overrightarrow{MA}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | c<a<b | C. | c<b<a | D. | b<c<a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2个 | B. | 4个 | C. | 5个 | D. | 6个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com