
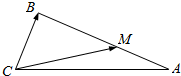
 如图,在△ABC中,|$\overrightarrow{CA}$|=6,|$\overrightarrow{CB}$|=3,M为线段AB上的一点,且|$\overrightarrow{CM}$|=x•$\overrightarrow{CA}$+y•$\overrightarrow{CB}$,$\overrightarrow{BM}$=2$\overrightarrow{MA}$.
如图,在△ABC中,|$\overrightarrow{CA}$|=6,|$\overrightarrow{CB}$|=3,M为线段AB上的一点,且|$\overrightarrow{CM}$|=x•$\overrightarrow{CA}$+y•$\overrightarrow{CB}$,$\overrightarrow{BM}$=2$\overrightarrow{MA}$.分析 (1)利用平面向量的三角形法则对向量$\overrightarrow{CM}$在CA,CB方向上分解,利用平面向量基本定理得到x,y;
(2)运用数量积的定义,将等式用$\overrightarrow{CA}$与$\overrightarrow{CB}$表示,即可得到所求.
解答 解:(1)由已知得$\overrightarrow{CM}=\overrightarrow{CB}+\overrightarrow{BM}=\overrightarrow{CB}+\frac{2}{3}\overrightarrow{BA}$=$\overrightarrow{CB}+\frac{2}{3}(\overrightarrow{CA}-\overrightarrow{CB})$=$\frac{2}{3}\overrightarrow{CA}+\frac{1}{3}\overrightarrow{CB}$=x•$\overrightarrow{CA}$+y•$\overrightarrow{CB}$,所以x=$\frac{2}{3}$,y=$\frac{1}{3}$;
(2)设$\overrightarrow{CA}$与$\overrightarrow{CB}$的夹角为θ,
因为$\overrightarrow{CM}$•$\overrightarrow{AB}$=-18,由(1)得到($\frac{2}{3}\overrightarrow{CA}+\frac{1}{3}\overrightarrow{CB}$)$•(\overrightarrow{CB}-\overrightarrow{CA})$=-18,
展开得$-\frac{2}{3}{\overrightarrow{CA}}^{2}+\frac{1}{3}{\overrightarrow{CB}}^{2}+\frac{1}{3}\overrightarrow{CA}•\overrightarrow{CB}$=-18,所以$-\frac{2}{3}×36+\frac{1}{3}×9+\frac{1}{3}×6×3×cosθ$=-18,解得cosθ=$\frac{1}{2}$,θ∈[0,π],所以θ=60°;
所以$\overrightarrow{CA}$与$\overrightarrow{CB}$的夹角为60°.
点评 本题考查平面向量的数量积的定义和性质,以及平面向量基本定理,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 偶函数,奇函数 | B. | 奇函数,偶函数 | C. | 偶函数,偶函数 | D. | 奇函数,奇函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m⊆A | B. | m∉A | C. | {m}∈A | D. | {m}⊆A |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com