
分析 (1)利用递推关系与等差数列的定义即可得出;
(2)利用“错位相减法”、等比数列的前n项和公式即可得出.
解答 解:(1)由Sn+Sn-2=2Sn-1+2(n≥3)知:Sn-Sn-1=Sn-1-Sn-2+2,
∴an=an-1+2,∴an-an-1=2(n≥3).
又∵a2-a1=2,
故an-an-1=2(n≥2),
∴{an}为等差数列.
(2)由(1)知,${a_n}=2n+1∴{b_n}=\frac{2n+1}{3^n}$,
∴${T_n}={b_1}+{b_2}+…+{b_n}=3×\frac{1}{3}+5×\frac{1}{3^2}+…+({2n+1})×\frac{1}{3^n}$ ①
$\frac{1}{3}{T_n}=3×\frac{1}{3^2}+5×\frac{1}{3^3}+…+(2n+1)×\frac{1}{{{3^{n+1}}}}$ ②
①-②得:$\frac{2}{3}{T_n}=3×\frac{1}{3}+2×\frac{1}{3^2}+2×\frac{1}{3^3}+…+2×\frac{1}{3^n}-(2n+1)×\frac{1}{{{3^{n+1}}}}$,
∴$\frac{2}{3}{T_n}=\frac{1}{3}+2({\frac{{\frac{1}{3}(1-\frac{1}{3^n})}}{{1-\frac{1}{3}}}})-(2n+1)×\frac{1}{{{3^{n+1}}}}=\frac{4}{3}-\frac{1}{3^n}-(2n+1)•\frac{1}{{{3^{n+1}}}}$,
∴${T_n}=2-(n+2)•\frac{1}{3^n}$.
点评 数列的诸多递推关系中,项与和之间的关系是最基本的,根源性的关系.学生意识不到这种递推关系的形成原因,具体到解题中,往往想不到,用不上;同样,在诸多求和方法中,经典的错位相减法,亦是学生的困难之处.我们应该给学生不断灌输基本的,经典的东西.本题考查了“错位相减法”、等差数列与等比数列的通项公式及其前n项和公式、递推关系,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
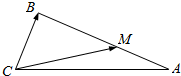 如图,在△ABC中,|$\overrightarrow{CA}$|=6,|$\overrightarrow{CB}$|=3,M为线段AB上的一点,且|$\overrightarrow{CM}$|=x•$\overrightarrow{CA}$+y•$\overrightarrow{CB}$,$\overrightarrow{BM}$=2$\overrightarrow{MA}$.
如图,在△ABC中,|$\overrightarrow{CA}$|=6,|$\overrightarrow{CB}$|=3,M为线段AB上的一点,且|$\overrightarrow{CM}$|=x•$\overrightarrow{CA}$+y•$\overrightarrow{CB}$,$\overrightarrow{BM}$=2$\overrightarrow{MA}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5π}{12}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com